Supertasks
A supertask is a task that consists in infinitely many component steps, but which in some sense is completed in a finite amount of time. Supertasks were studied by the pre-Socratics and continue to be objects of interest to modern philosophers, logicians and physicists. The term “super-task” itself was coined by J.F. Thomson (1954).
Here we begin with an overview of the analysis of supertasks and their mechanics. We then discuss the possibility of supertasks from the perspective of general relativity.
- 1. Mechanical properties
- 2. Supertasks in Relativistic Spacetime
- Bibliography
- Academic Tools
- Other Internet Resources
- Related Entries
1. Mechanical properties
Strange things can happen when one carries out an infinite task.
For example, consider a hotel with a countably infinite number of rooms. One night when the hotel is completely occupied, a traveler shows up and asks for a room. “No problem,” the receptionist replies, “there’s plenty of space!” The first occupant then moves to the second room, the second to the third room, the third to the fourth room, and so on all the way up. The result is a hotel that has gone from being completely occupied to having one room free, and the traveler can stay the night after all. This supertask was described in a 1924 lecture by David Hilbert, as reported by Gamow (1947).
One might take such unusual results as evidence against the possibility of supertasks. Alternatively, we might take them to seem strange because our intuitions are based on experience with finite tasks, and which break down in the analysis of supertasks. For now, let us simply try to come to grips with some of the unusual mechanical properties that supertasks can have.
1.1 Missing final and initial steps: The Zeno walk
Supertasks often lack a final or initial step. A famous example is the first of Zeno’s Paradoxes, the Paradox of the Dichotomy. The runner Achilles begins at the starting line of a track and runs ½ of the distance to the finish line. He then runs half of the remaining distance, or ¼ of the total. He then runs half the remaining distance again, or ⅛ of the total. And he continues in this way ad infinitum, getting ever-closer to the finish line (Figure 1.1.1). But there is no final step in this task.
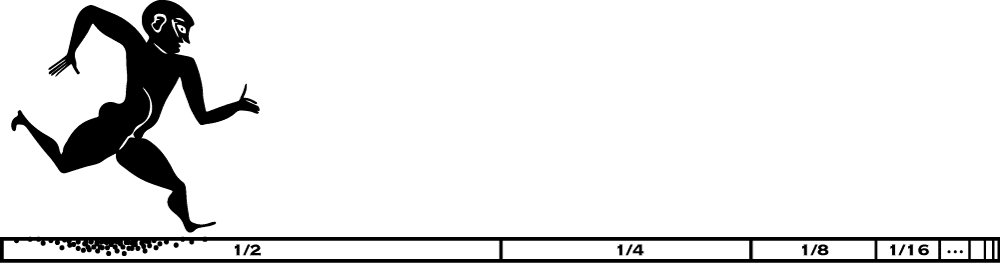
Fig 1.1.1. The Zeno Dichotomy supertask.
There is also a “regressive” version of the Dichotomy supertask that has no initial step. Suppose that Achilles does reach the finish line. Then he would have had to travel the last ½ of the track, and before that ¼ of the track, and before that ⅛ of the track, and so on. In this description of the Achilles race, we imagine winding time backwards and viewing Achilles getting ever-closer to the starting line (Figure 1.1.2). But now there is no initial step in the task.

Fig 1.1.2. Regressive version of the Zeno Dichotomy supertask.
Zeno, at least as portrayed in Aristotle’s Physics, argued that as a consequence, motion does not exist. Since an infinite number of steps cannot be completed, Achilles will never reach the finish line (or never have started in the regressive version). However, modern mathematics provides ways of explaining how Achilles can complete this supertask. As Salmon (1998) has pointed out, much of the mystery of Zeno’s walk is dissolved given the modern definition of a limit. This provides a precise sense in which the following sum converges:
\[ \frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \frac{1}{16} + \cdots . \]Although it has infinitely many terms, this sum is a geometric series that converges to 1 in the standard topology of the real numbers. A discussion of the philosophy underpinning this fact can be found in Salmon (1998), and the mathematics of convergence in any real analysis textbook that deals with infinite series. From this perspective, Achilles actually does complete all of the supertask steps in the limit as the number of steps goes to infinity. One might only doubt whether or not the standard topology of the real numbers provides the appropriate notion of convergence in this supertask. A discussion of the subtleties of the choice of topology has been given by Mclaughlin (1998).
Max Black (1950) argued that it is nevertheless impossible to complete the Zeno task, since there is no final step in the infinite sequence. The existence of a final step was similarly demanded on a priori terms by Gwiazda (2012). But as Thomson (1954) and Earman and Norton (1996) have pointed out, there is a sense in which this objection equivocates on two different meanings of the word “complete.” On the one hand “complete” can refer to the execution of a final action. This sense of completion does not occur in Zeno’s Dichotomy, since for every step in the task there is another step that happens later. On the other hand, “complete” can refer to carrying out every step in the task, which certainly does occur in Zeno’s Dichotomy. From Black’s argument one can see that the Zeno Dichotomy cannot be completed in the first sense. But it can be completed in the second. The two meanings for the word “complete” happen to be equivalent for finite tasks, where most of our intuitions about tasks are developed. But they are not equivalent when it comes to supertasks.
Hermann Weyl (1949, §2.7) suggested that if one admits that the Zeno race is possible, then one should equally admit that it is possible for a machine to carry out an infinite number of tasks in finite time. However, one difference between the Zeno run and a machine is that the Zeno run is continuous, while the tasks carried out by a machine are typically discrete. This led Grünbaum (1969) to consider the “staccato” version of the Zeno run, in which Achilles pauses for successively shorter times at each interval.
1.2 Missing limits: Thomson’s Lamp
Supertasks are often described by sequences that do not converge. J. F. Thomson (1954) introduced one such example now known as Thomson’s Lamp, which he thought illustrated a sense in which supertasks truly are paradoxical.
Suppose we switch off a lamp. After 1 minute we switch it on. After ½ a minute more we switch it off again, ¼ on, ⅛ off, and so on. Summing each of these times gives rise to an infinite geometric series that converges to 2 minutes, after which time the entire supertask has been completed. But when 2 minutes is up, is the lamp on or off?
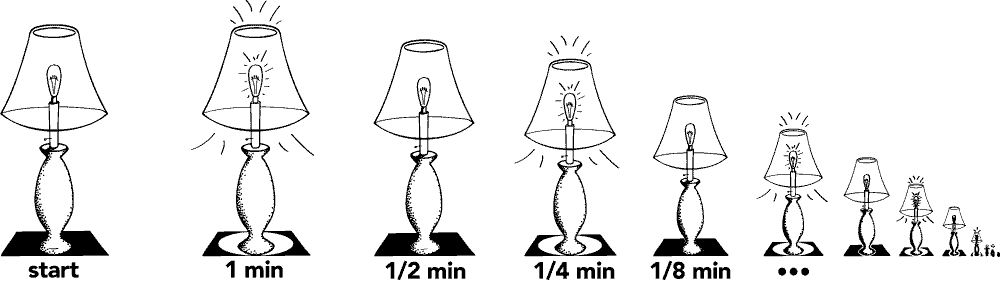
Fig 1.2.1. Thomson’s lamp.
It may seem absurd to claim that it is on: for each moment that the lamp was turned on, there is a later moment at which it was turned off. But it would seem equally absurd to claim that it is off: for each moment that the lamp is turned off, there is a later moment that it was turned on. This paradox, according to Thomson, suggests that the supertask associated with the lamp is impossible.
To analyze the paradox, Thomson suggested we represent the “on” state of the map with the number 1 and the “off” state with 0. The supertask then consists in the sequence of states,
\[ 0, 1, 0, 1, 0, 1, \ldots . \]This sequence does not converge to any real number in the standard real topology. However, one might redefine what it means for a sequence to converge in response to this. For example, we could define convergence in terms of the arithmetic mean. Given a sequence \(x_n\), the Cesàro mean is the sequence \(C_1 = x_1\), \(C_2 = (x_1 + x_2)/2\), \(C_3 = (x_1 + x_2 + x_3)/3\), and so on. These numbers describe the average value of the sequence up to a given term. One says that a sequence \(x_n\) Cesàro converges to a number \(C\) if and only if \(C_n\) converges (in the ordinary sense) to \(C\). It is then well-known that the sequence \(0, 1, 0, 1, \ldots\) Cesàro converges to ½ (see e.g. Bashirov 2014).
Thomson pointed out that this argument is not very helpful without an interpretation of what lamp-state is represented by ½. We want to know if the lamp is on or off; saying that its end state is associated with a convergent arithmetic mean of ½ does little to answer the question. However, this approach to resolving the paradox has still been pursued, for example by Pérez Laraudogoita, Bridger and Alper (2002) and by Dolev (2007).
Are there other consistent ways to describe the final state of Thomson’s lamp in spite of the missing limit?
Benacerraf (1962) pointed out a sense in which the answer is yes. The description of the Thomson lamp only actually specifies what the lamp is doing at each finite stage before 2 minutes. It says nothing about what happens at 2 minutes, especially given the lack of a converging limit. It may still be possible to “complete” the description of Thomson’s lamp in a way that leads it to be either on after 2 minutes or off after 2 minutes. The price is that the final state will not be reached from the previous states by a convergent sequence. But this by itself does not amount to a logical inconsistency.
Such a completion of Thomson’s description was explicitly constructed by Earman and Norton (1996) using the following example of a bouncing ball.
Suppose a metal ball bounces on a conductive plate, bouncing a little lower each time until it comes to a rest on the plate. Suppose the bounces follow the same geometric pattern as before. Namely, the ball is in the air for 1 minute after the first bounce, ½ minute after the second bounce, ¼ minute after the third, ⅛ minute after the fourth, and so on. Then the entire infinite sequence of bounces is a supertask.
Now suppose that the ball completes a circuit when it strikes the metal plate, thereby switching on a lamp. This is a physical system that implements Thomson’s lamp. In particular, the lamp is switched on and off infinitely many times over the course of a finite duration of 2 minutes.
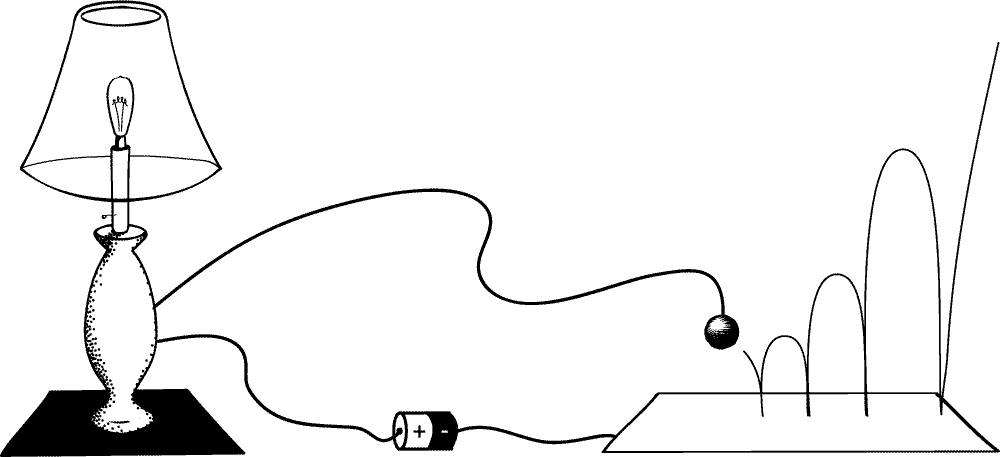
Fig 1.2.2. Thomson’s lamp implemented by a bouncing ball: contact of the bouncing ball with the plate switches the Thomson lamp on. The supertask ends with the lamp on.
What is the state of this lamp after 2 minutes? The ball will have come to rest on the plate, and so the lamp will be on. There is no mystery in this description of Thomson’s lamp.
Alternatively, we could arrange the ball so as to break the circuit when it makes contact with the plate. This gives rise to another implementation of Thomson’s lamp, but one that is off after 2 minutes when the ball comes to its final resting state.
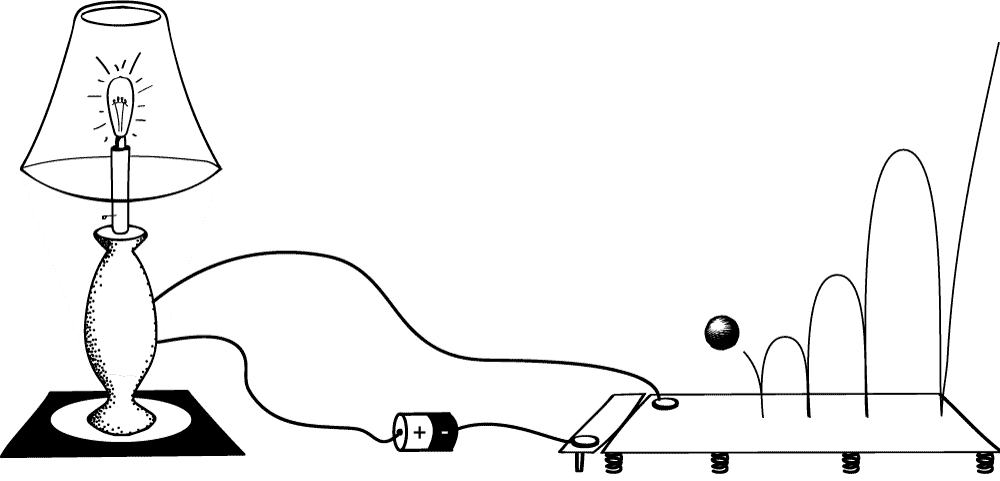
Fig 1.2.3. Another implementation of Thomson’s lamp: contact of the bouncing ball with the plate switches the Thomson lamp off. The supertask ends with the lamp off.
These examples show that is possible to fill in the details of Thomson’s lamp in a way that either renders it definitely on after the supertask, or definitely off. For this reason, Earman and Norton conclude with Benacerraf that the Thomson lamp is not a matter of paradox but of an incomplete description.
As with the Zeno Dichotomy, there is a regressive version of the Thomson lamp supertask. Such a lamp has been studied by Uzquiano (2012), although as a set of instructions rather than a set of tasks. Consider a lamp that has been switched on at 2 seconds past the hour, off at 1 second past, on at ½ a second past, off at ¼ a second past, and so on. What is the state of the lamp on the hour, just before the supertask has begun? This supertask can be viewed as incomplete in the same way as the original Thomson lamp. Insofar as the mechanics of bouncing balls and electric circuits described in Earman and Norton’s lamp are time reversal invariant, it follows that the time-reversed system is a possibility as well, which is spontaneously excited to begin bouncing, providing a physical implementation of the regressive Thomson lamp. However, whether the reversed Thomson lamp is a physical possibility depends on whether or not the system is time reversible. A difficulty is that its initial state will not determine the subsequent history of an infinity of alternations.
1.3 Discontinuous quantities: The Littlewood-Ross Paradox
Sometimes supertasks require a physical quantity to be discontinuous in time. One example of this, known as Ross’ paradox, was described by John Littlewood (1953) as an “infinity paradox” and expanded upon by Sheldon Ross (1988) in his well-known textbook on probability. It goes as follows.
Suppose we have a jar—a very large jar—with the capacity to hold infinitely many balls. We also have a countably infinite pile of balls, numbered 1, 2, 3, 4, …. First we drop balls 1–10 into the jar, then remove ball 1. (This adds a total of nine balls to the jar.) Then we drop balls 11–20 in the jar, and remove ball 2. (This brings the total up to eighteen.) Suppose that we continue in this way ad infinitum, and that we do so with ever-increasing speed, so that we will have used up our entire infinite pile of balls in finite time (Figure 1.3.1). How many balls will be in the jar when this supertask is over?
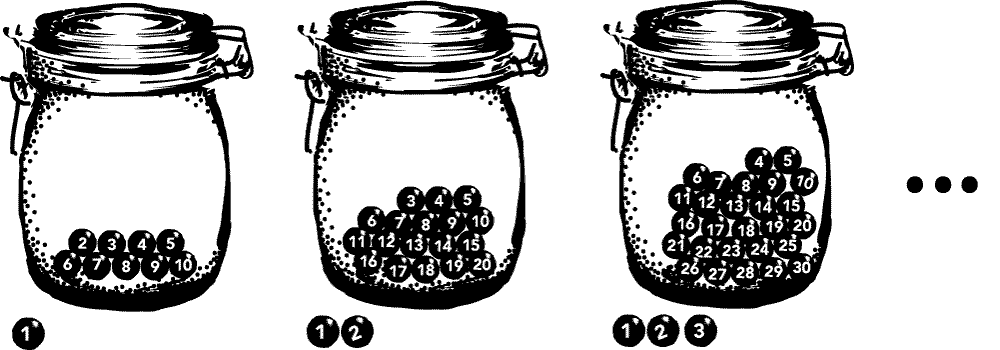
Fig 1.3.1. The Littlewood-Ross procedure.
Both Littlewood (1953) and Ross (1976) responded that the answer is zero. Their reasoning went as follows.
Ball 1 was removed at the first stage. Ball 2 was removed at the second stage. Ball n was removed at the nth stage, and so on ad infinitum. Since each ball has a label n, and since each label n was removed at the nth stage of the supertask, there can be only be zero balls left in the jar at the end after every stage has been completed. One can even identify the moment at which each of them was removed.
Some may be tempted to object that, on the contrary, the number of balls in the jar should be infinite when the supertask is complete. After the first stage there are 9 balls in the jar. After the second stage there are 18. After the third stage there are 27. In the limit as the number of stages approaches infinity, the total number of balls in the jar diverges to infinity. If the final state of the jar is determined by what the finite-stage states are converging to, then the supertask should conclude with infinitely many balls in the jar.
If both of these responses are equally reasonable, then we have a contradiction. There cannot be both zero and infinity balls in a jar. It is in this sense that the Littlewood-Ross example might be a paradox.
Allis and Koetsier (1991) argued that only the first response is justified because of a reasonable “principle of continuity”: that the positions of the balls in space are a continuous function of time. Without such a principle, the positions of the balls outside the jar could be allowed to teleport discontinuously back into the jar as soon as the supertask is complete. But with such a principle in place, one can conclude that the jar must be empty at the end of the supertask. This principle has been challenged by Van Bendegum (1994), with a clarifying rejoinder by Allis and Koetsier (1996).
Earman and Norton (1996) follow Allis and Koetsier (and Littlewood and Ross) in demanding that the worldlines of the balls in the jar be continuous, but point out that there is a different sense of discontinuity that develops as a consequence. (A ‘worldline’ is used here to describe the trajectory of a particle through space and time; it is discussed more below in the section on Time in Relativistic Spacetime.) Namely, if one views the number of balls in the jar as approximated by a function \(N(t)\) of time, then this “number function” is discontinuous in the Littlewood-Ross supertask, blowing up to an arbitrarily large value over the course of the supertask before dropping discontinuously to 0 once it is over. In this sense, the Littlewood-Ross paradox presents us with a choice, to either,
- Take the worldline of each ball in the jar to be continuous in time; or
- Take the number \(N(t)\) of balls in the jar to be approximated by a continuous function of time;
but not both. The example thus seems to require a physical quantity to be discontinuous in time: either in the worldlines of the balls, or in the number of balls in the jar.
A variation of the Littlewood-Ross example has been posed as a puzzle for decision theory by Barrett and Arntzenius (1999, 2002). They propose a game involving an infinite number of $1 bills, each numbered by a serial number 1, 2, 3, …, and in which a person begins with $0. The person must then choose between the following two options.
- Option A: accept $1; or
- Option B: first accept $2n+1, where n is the number of times the offer has been made, and then return whatever bill the player holds with the smallest serial number.
At each finite stage of the game it appears to be rational to choose Option B. For example, at stage n=1 Option B returns $3, while Option A returns $1. At stage n=2 Option B returns $7 while Option A returns $1. And so on.
However, suppose that one plays this game as a supertask, so that the entire infinite number of offers is played in finite time. Then how much money will the player have? Following exactly the same reasoning as in the Littlewood-Ross paradox, we find that the answer is $0. For each bill’s serial number, there is a stage at which that bill was returned. So, if we presume the worldlines of the bills must be continuous, then the infinite game ends with the player winning nothing at all. This is a game in which the rational strategy at each finite stage does not provide a winning strategy for the infinite game.
There are variations on this example that have a more positive yield for the players. For example, Earman and Norton (1996) propose the following pyramid marketing scheme. Suppose that an agent sells two shares of a business for $1,000 each to a pair of agents. Each agent splits their share in two and sells it for $2,000 to two more agents, thus netting $1,000 while four new agents go into debt for $1,000 each. Each of the four new agents then do the same, and so on ad infinitum. How does this game end?
If the pool of agents is only finitely large, then the last agents will get saddled with the debt while all the previous agents make a profit. But if the pool is infinitely large, and the pyramid marketing scheme becomes a supertask, then all of the agents will have profited when it is completed. At each stage in which a given agent is in debt, there is a later stage in which the agent sells to shares and makes $1,000. This is thus a game that starts with equal total amount of profit and debt, but concludes having converted the debt into pure profit.
1.4 Classical mechanical supertasks
The discussions of supertasks so far suggest that the possibility of supertasks is not so much a matter of logical possibility as it is “physical possibility.” But what does “physical possibility” mean? One natural interpretation is that it means, “possible according to some laws of physics.” Thus, we can make the question of whether supertasks are possible more precise by asking, for example, whether supertasks compatible with the laws of classical particle mechanics.
Earman and Norton’s (1996) bouncing ball provides one indication that the answer is yes. Another particularly simple example was introduced by Pérez Laraudogoita (1996, 1998), which goes as follows.
Suppose an infinite lattice of particles of the same mass are arranged so that there is a distance of ½ between the first and the second, a distance of ¼ between the second and the third, a distance of ⅛ between the third and the fourth, and so on. Now imagine that a new particle of the same mass collides with the first particle in the lattice, as in Figure 1.4.1. If it is a perfectly elastic collision, then the incoming particle will come to rest and the velocity will be transferred to the struck particle. Suppose it takes ½ of a second for the second collision to occur. Then it will take ¼ of a second for the third to occur, ⅛ of a second for the fourth, and so on. The entire infinite process will thus be completed after 1 second.

Fig 1.4.1. Jon Pérez Laraudogoita’s ‘Beautiful Supertask’
Earman and Norton (1998) observed several curious facts about this system. First, unlike Thomson’s lamp, this supertask does not require unbounded speeds. The total velocity of the system is never any more than the velocity of the original moving particle. Second, this supertask takes place in a bounded region of space. So, there are no boundary conditions “at infinity” that can rule out the supertask. Third, although energy is conserved in each local collision, the global energy of this system is not conserved, since after finite time it becomes a lattice of infinitely many particles all at rest. Finally, the supertask depends crucially on there being an infinite number of particles, and the width of these particles must shrink without bound while keeping the mass fixed. This means the mass density of the particles must grow without bound. The failure of global energy conservation and other curious features of this system have been studied by Atkinson (2007, 2008), Atkinson and Johnson (2009, 2010) and by Peijnenburg and Atkinson (2008) and Atkinson and Peijnenburg (2014).
Another kind of classical mechanical supertask was described by Pérez Laraudogoita (1997). Consider again the infinite lattice of particles of the same mass, but this time suppose that the first particle is motionless, that the second particle is headed towards the first with some velocity, and that the velocity of each successive particle doubles (Figure 1.4.2). The first collision sets the first particle in motion. But a later collision then sets it moving faster, and a later collision even faster, and so on.

Fig 1.4.2. A supertask that relies on unbounded speed.
It is not hard to arrange this situation so that the first collision happens after ½ of a second, the second collision after ¼ of a second, the third after ⅛ of a second, and so on (Pérez Laraudogoita 1997). So again we have a supertask that is completed after one second.
What is the result of this supertask? Their answer is that none of the particles remain in space. They cannot be anywhere in space, since for each horizontal position that a given particle can occupy there is a time before 1 second that it is pushed out of that position by a collision. The worldline of any one of the particles from this supertask can be illustrated using Figure 1.4.3. This is what Malament (2008, 2009) has referred to as a “space evader” trajectory. The time-reversed “space invader” trajectory is one in which the vacuum is spontaneously populated with particles after some fixed time.
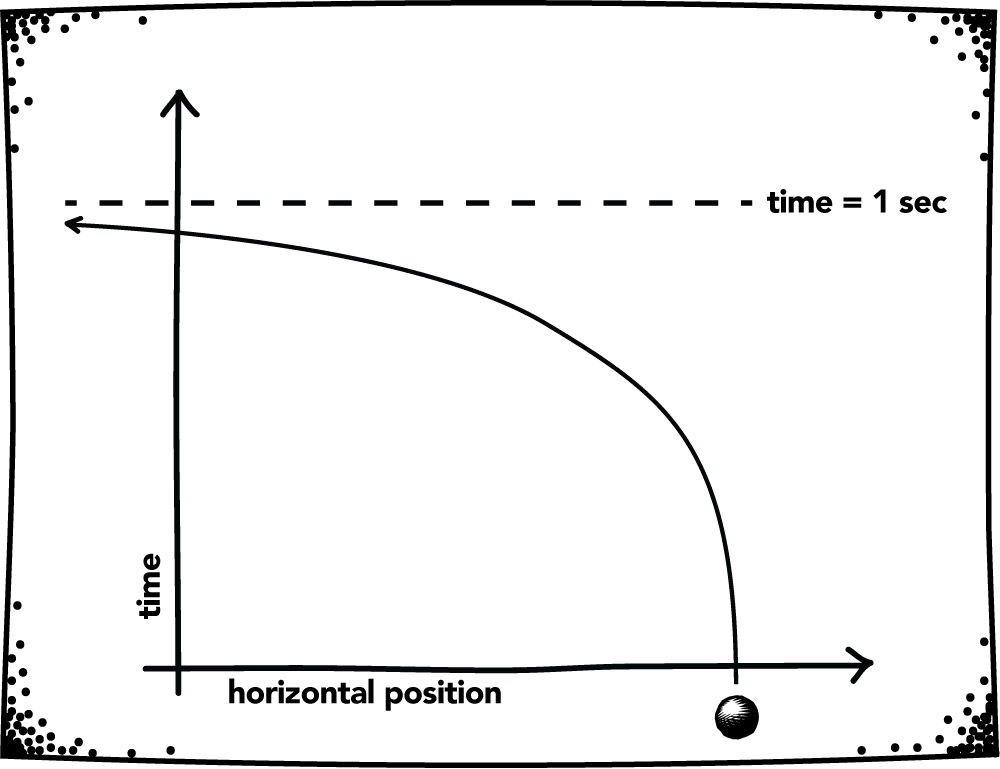
Fig 1.4.3. Worldline of the supertask particle.
Earman and Norton (1998) gave some variations on this supertask, including one which occurs in a bounded region in space. Unlike the example of Pérez Laraudogoita (1996), this supertask also essentially requires particles to be accelerated to arbitrarily high speeds, and in this sense is essentially non-relativistic. See Pérez Laraudogoita (1999) for a rejoinder.
This supertask is modeled on an example of Benardete (1964), who considered a space ship that successively doubles its speed until it escapes to spatial infinity. Supertasks of this kind were also studied by physicists like Lanford (1975, §4), who identified a system of particles colliding elastically that can undergo an infinite number of collisions in finite time. Mather and McGehee (1975) pointed out a similar example. Earman (1986) discussed the curious behavior of Lanford’s example as well, pointing out that such supertasks provide examples of classical indeterminism, but can be eliminated by restricting to finitely many particles or by imposing appropriate boundary conditions.
1.5 Quantum mechanical supertasks
It is possible to carry some of the above considerations of supertasks over from classical to quantum mechanics. The examples of quantum mechanical supertasks that have been given so far are somewhat less straightforward than the classical supertasks above. However, they also bear a more interesting possible relationship to physical experiments.
Example 1: Norton’s Lattice
Norton (1999) investigated whether there exists a direct quantum mechanical analogue of the kinds of supertasks discussed above. He began by considering the classical scenario shown in Figure 1.5.1 of an infinite lattice of interacting harmonic oscillators. Assuming the springs all have the same tension and solving the equation of motion for this system, Norton found that it can spontaneously excite, producing an infinite succession of oscillations in the lattice in a finite amount of time.

Fig 1.5.1. Norton’s infinite harmonic oscillator system.
Using this example as a model, Norton produced a similar supertask for a quantum lattice of harmonic oscillators. Begin with an infinite lattice of 2-dimensional quantum systems, each with a ground state \(\ket{\phi}\) and an excited state \(\ket{\chi}\). Consider the collection of vectors,
\[\begin{align} \ket{0} &= \ket{\phi} \otimes \ket{\phi} \otimes \ket{\phi} \otimes \ket{\phi} \otimes \cdots \\ \ket{1} &= \ket{\chi} \otimes \ket{\phi} \otimes \ket{\phi} \otimes \ket{\phi} \otimes \cdots \\ \ket{2} &= \ket{\phi} \otimes \ket{\chi} \otimes \ket{\phi} \otimes \ket{\phi} \otimes \cdots \\ \ket{3} &= \ket{\phi} \otimes \ket{\phi} \otimes \ket{\chi} \otimes \ket{\phi} \otimes \cdots \\ \ket{4} &= \ket{\phi} \otimes \ket{\phi} \otimes \ket{\phi} \otimes \ket{\chi} \otimes \cdots \\ \;\vdots& \end{align}\]For simplicity, we restrict attention to the possible states of the system that are spanned by this set. We posit a Hamiltonian that has the effect of leaving |0⟩ invariant; of creating |1⟩ and destroying |2⟩; of creating |2⟩ and destroying |3⟩; and so on. Norton then solved the differential form of the Schrödinger equation for this interaction and argued that it admits solutions in which all of the nodes in the infinite lattice start in their ground state, but all become spontaneously excited in finite time.
Norton’s quantum supertask requires a non-standard quantum system because the dynamical evolution he proposes is not unitary, even though it obeys a differential equation in wavefunction space that takes the form of the Schrödinger equation (Norton 1999, §5). Nevertheless, Norton’s quantum supertask has fruitfully appeared in physical applications, having been found to arise naturally in a framework for perturbative quantum field theory proposed by Duncan and Niedermaier (2013, Appendix B).
Example 2: Hepp Measurement
Although quantum systems may sometimes be in a pure superposition of measurable states, we never observe our measurement devices to be in such states when they interact with quantum systems. On the contrary, our measurement devices always seem to display definite values. Why? Hepp (1972) proposed to explain this by modeling the measurement process using a quantum supertask. This example was popularized by Bell (1987, §6) and proposed as a solution to the measurement problem by Wan (1980) and Bub (1988).
Here is a toy example illustating the idea. Suppose we model an idealised measuring device as consisting in an infinite number of fermions. We imagine that the fermions do not interact with each other, but that a finite number of them will couple to our target system whenever we make a measurement. Then an observable characterising the possible outcomes of a given measurement will be a product corresponding to some finite number n of observables,
\[ A = A_1 \otimes A_2 \otimes \cdots \otimes A_n \otimes I \otimes I \otimes I \otimes \cdots \]Restricting to a finite number of fermions at a time has the effect of splitting the Hilbert space of states into special subspaces called superselection sectors, which have the property that when \(\ket{\psi}\) and \(\ket{\phi}\) come from different sectors, any superposition \(a\ket{\psi} + b\ket{\phi}\) with \(|a|^2 + |b|^2 = 1\) will be a mixed state. It turns out in particular that the space describing the state in which all the fermions are \(z\)-spin-up is in a different superselection sector than the space in which they are all spin down. Although this may be puzzling for the newcomer, it can be found in any textbook that deals with superselection. And it allows us to construct an interesting supertask describing the measurement process. The following simplified version of it was given by Bell (1987).
Suppose we wish to measure a single fermion. We model this as a wavefunction that zips by the locations of each fermion in our measurement device, interacting locally with the individual fermions in the device as it goes (Figure 1.5.2). The interaction is set up in such a way that every fermion is passed in finite time, and such that after the process is completed, the measurement device indicates what the original state of the fermion being measured was. In particular, suppose the single fermion begins in a \(z\)-spin-up state. Then, after it has zipped by each of the infinite fermions, they will all be found in the \(z\)-spin-up state. If the single fermion begins in a \(z\)-spin-down state, then the infinite collection of fermions would all be \(z\)-spin-down. What if the single fermion was in a superposition? Then the infinite collection of fermions would contain some mixture of \(z\)-spin up and \(z\)-spin down states.
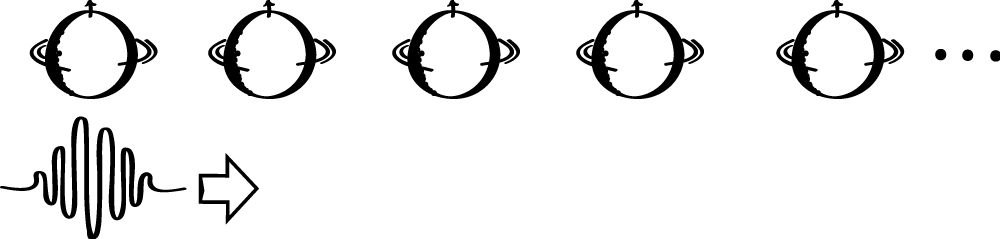
Fig 1.5.2. Bell’s implementation of the Hepp measurement supertask.
Hepp found that, because of the superselection structure of this system, this measurement device admits mixed states that can indicate the original state of the single fermion, even when the latter begins in a pure superposition. Suppose we denote the \(z\)-spin observable for the nth fermion in the measurement device as, \(s_n = I \otimes I \otimes \cdots (n\,times) \cdots \otimes \sigma_z \otimes I \cdots.\) We now construct a new observable, given by,
\[ S = \lim_{n\rightarrow\infty} \tfrac{1}{n}(s_1 + s_2 + \cdots + s_n). \]This observable has the property that \(\langle \psi, S\phi\rangle = 1\) if \(\ket{\psi}\) and \(\ket{\phi}\) both lie in the same superselection sector as the state in which all the fermions in the measurement device are \(z\)-spin-up. It also has the property that \(\langle\psi,S\phi\rangle = -1\) if they lie in the same superselection sector as the all-down state. But more interestingly, suppose the target fermion that we want to measure is in a pure superposition of \(z\)-spin-up and \(z\)-spin-down states. Then, after it zips by all the fermions in the measurement device, that measurement device will be left in a superposition of the form \(a\ket{\uparrow} + b\ket{\downarrow}\), where \(\ket{\uparrow}\) is the state in which all the fermions in the device are spin-up and \(\ket{\downarrow}\) is the state in which they are all spin down. Since \(\ket{\uparrow}\) and \(\ket{\downarrow}\) are in different superselection sectors, it follows that their superposition must be a mixed state. In other words, this model allows the measurement device to indicate the pure state of the target fermion, even when that state is a pure superposition, without the device itself being in a pure superposition.
The supertask underpinning this model requires an infinite number of interactions. As Hepp and Bell described it, the model was unrealistic because it required an infinite amount of time. However, a similar system was shown by Wan (1980) and Bub (1988) to take place in finite time. Their approach appears at first glance to be a promising model of measurement. However, Landsman (1991) pointed out that it is inadequate on one of two levels: either the dynamics is not automorphic (which is the analogue of unitarity for such systems), or the task is not completed in finite time. Landsman (1995) has argued that neither of these two outcomes is plausible for a realistic local description of a quantum system.
Example 3: Continuous Measurement
Another quantum supertask is found in the so-called Quantum Zeno Effect. This literature begins with a question: what would happen if we were to continually monitor a quantum system, like an unstable atom? The predicted effect is that the system would not change, even if it is an unstable atom that would otherwise quickly decay.
Misra and Sudarshan (1977) proposed to make the concept of “continual monitoring” precise using a Zeno-like supertask. Imagine that an unstable atom is evolving according to some law of unitary evolution \(U_t\). Suppose we measure whether or not the atom has decayed by following that regressive form of Zeno’s Dichotomy above. Namely, we measure it at time \(t\), but also at time \(t/2\), and before that at time \(t/4\), and at time \(t/8\), and so on. Let \(E\) be a projection corresponding to the initial undecayed state of the particle. Finding the atom undecayed at each stage in the supertask then corresponds to the sequence,
\[ EU_tE,\; EU_{t/2}E,\; EU_{t/4}E,\; EU_{t/8}E,\ldots. \]Misra and Sudarshan use this sequence as a model for continuous measurement, by supposing that the sequence above converges to an operator \(T(t)=E\), and that it does so for all times \(t\) greater than or equal to zero. The aim is for this to capture the claim that the atom is continually monitored beginning at a fixed time \(t=0\). They prove from this assumption that, for most reasonable quantum systems, if the initial state is undecayed in the sense that \(\mathrm{Tr}(\rho E)=1\), then the probability that the atom will decay in any given time interval \([0,t]\) is equal to zero. That is, continual monitoring implies that the atom will never decay.
These ideas have given rise to a large literature of responses. To give a sampling: Ghirardi et al. (1979) and Pati (1996) have objected that this Zeno-like model of a quantum measurement runs afoul of other properties of quantum theory, such as the time-energy uncertainty relations, which they argue should prevent the measurements in the supertask sequence above from being made with arbitrarily high frequency. Bokulich (2003) has responded that, nevertheless, such a supertask can still be carried out when the measurement commutes with the unitary evolution, such as when \(E\) is a projection onto an energy eigenstate.
2. Supertasks in Relativistic Spacetime
In Newtonian physics, time passes at the same rate for all observers. If Alice and Bob are both present at Alice’s 20th and 21st birthday parties, both people will experience an elapsed time of one year between the two events. (This is true no matter what Alice or Bob do or where Alice and Bob go in between the two events.) Things aren’t so simple in relativistic physics. Elapsed time between events is relative to the path through spacetime a person takes between them. It turns out that this fact opens up the possibility of a new type of supertask. Let’s investigate this possibility in a bit more detail.
2.1 Time in Relativistic Spacetime
A model of general relativity, a spacetime, is a pair \((M,g)\). It represents a possible universe compatible with the theory. Here, \(M\) is a manifold of events. It gives the shape of the universe. (Lots of two-dimensional manifolds are familiar to us: the plane, the sphere, the torus, etc.) Each point on \(M\) represents a localized event in space and time. A supernova explosion (properly idealized) is an event. A first kiss (properly idealized) is also an event. So is the moon landing. But July 20, 1969 is not an event. And the moon is not an event.
Manifolds are great for representing events. But the metric \(g\) dictates how these events are related. Is it possible for a person to travel from this event to that one? If so, how much elapsed time does a person record between them? The metric \(g\) tells us. At each event, \(g\) assigns a double cone structure. The cone structures can change from event to event; we only require that they do so smoothly. Usually, one works with models of general relativity in which one can label the two lobes of each double cone as “past” and “future” in a way which involves no discontinuities. We will do so in what follows. (See figure 2.1.1.)
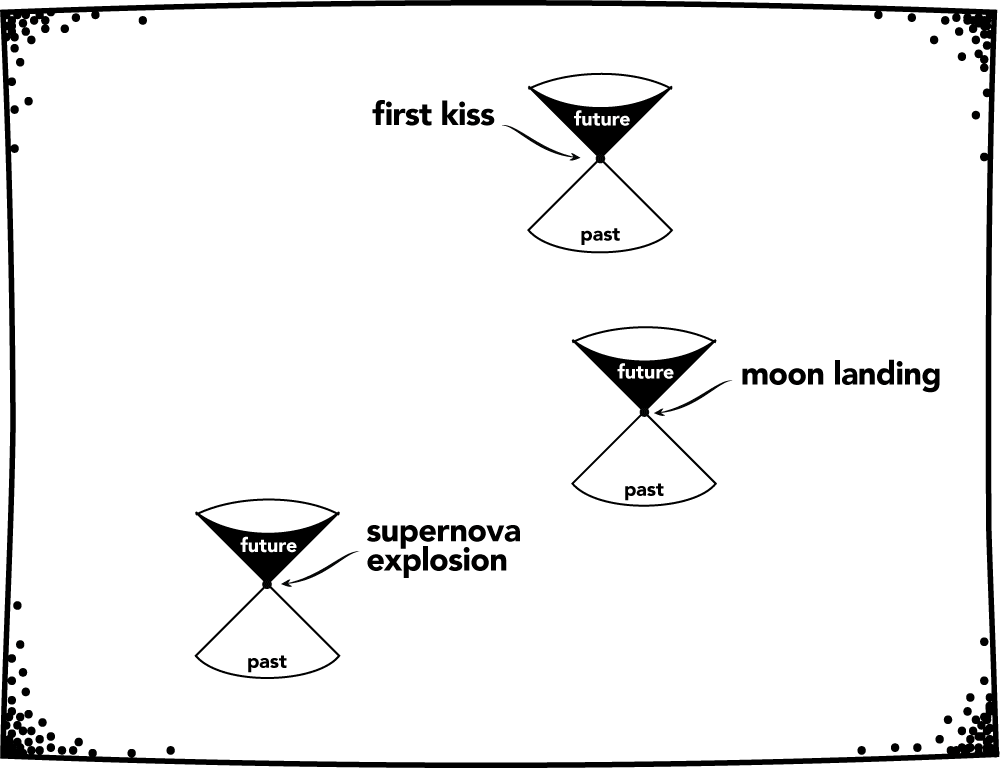
Fig 2.1.1. Events in spacetime and the associated double cones.
Intuitively, the double cone structure at an event demarcates the speed of light. Trajectories through spacetime which thread the inside of the future lobes of these “light cones” are possible routes in which travel stays below the speed of light. Such a trajectory is a worldline and, in principle, can be traversed by a person. Now, some events cannot be connected by a worldline. But if two events can be connected by a worldline, there is an infinite number of worldlines which connect them.
Each worldline has a “length” as measured by the metric \(g\); this length is the elapsed time along the worldline. Take two events on a manifold \(M\) which can be connected by a worldline. The elapsed time between the events might be large along one worldline and small along another. Intuitively, if a worldline is such that it stays close to the boundaries of the cone structures (i.e. if the trajectory stays “close to the speed of light”), then the elapsed time is relatively small. (See Figure 2.1.2.) In fact, it turns out that if two events can be connected by a worldline, then for any number \(t>0\), there is a worldline connecting the events with an elapsed time less than \(t\)!
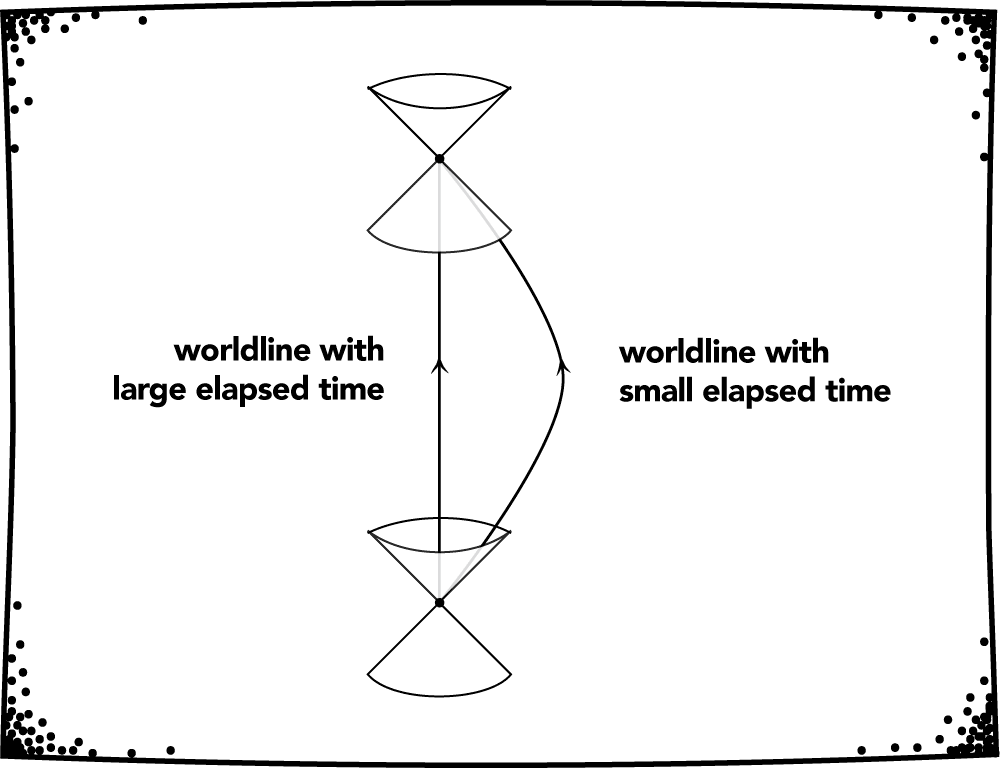
Fig 2.1.2. Elapsed time is worldline dependent.
2.2 Malament-Hogarth Spacetimes
The fact that, in relativistic physics, elapsed time is relative to worldlines suggests a new type of bifurcated supertask. The idea is simple. (A version of the following idea is given in Pitowsky 1990.) Two people, Alice and Bob, meet at an event \(p\) (the start of the supertask). Alice then follows a worldline with a finite elapsed time which ends at a given event \(q\) (the end of the supertask). On the other hand, Bob goes another way; he follows a worldline with an infinite elapsed time. Bob can use this infinite elapsed time to carry out a computation which need not halt after finitely many steps. Bob might check all possible counterexamples to Goldbach’s conjecture, for example. (Goldbach’s conjecture is the statement that every even integer n which is greater than 2 can be expressed as the sum of two primes. It is presently unknown whether the conjecture is true. One could settle it by sequentially checking to see if each instantiated statement is true for \(n=4\), \(n=6\), \(n=8\), \(n=10\), and so on.) If the computation halts, then Bob sends a signal to Alice at \(q\) saying as much. If the computation fails to halt, no such signal is sent. The upshot is that Alice, after a finite amount of elapsed time, knows the result of the potentially infinite computation at \(q\).
Let’s work a bit more to make the idea precise. We say that a half-curve is a worldline which starts at some event and is extended as far as possible in the future direction. Next, the observational past of an event q, OP(q), is the collection of all events x such that there a is a worldline which starts at x and ends at q. Intuitively, a (slower than light) signal may be sent from an event x to an event q if and only if x is in the set OP(q). (See figure 2.2.1.)
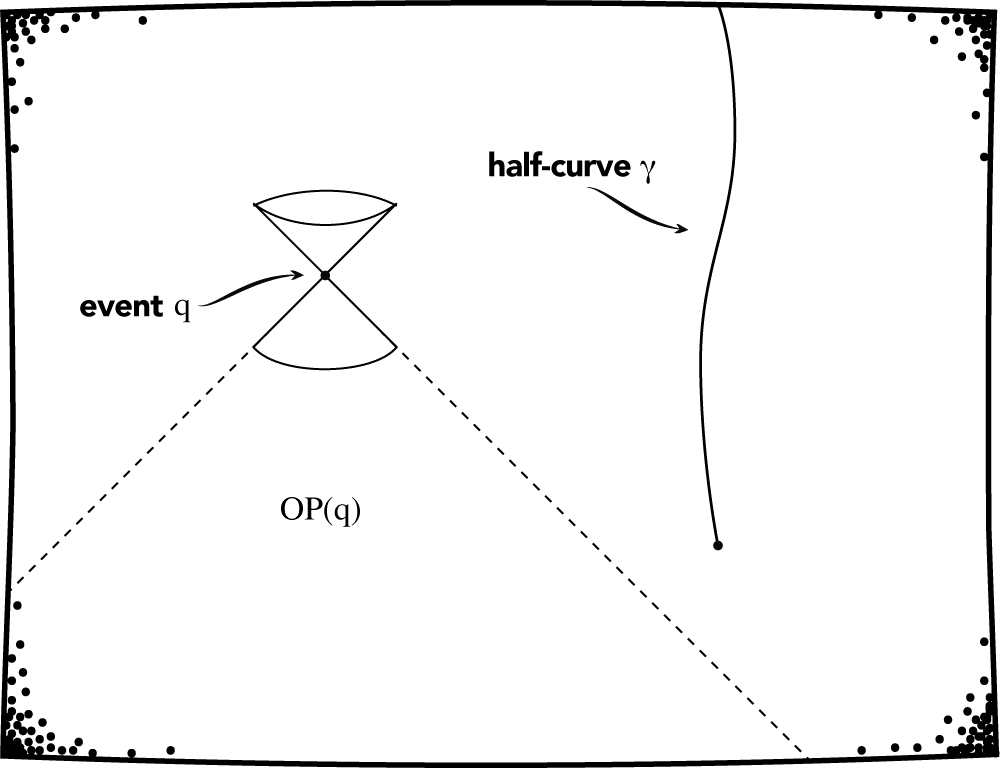
Fig 2.2.1. The observational past of an event and a half-curve. A signal can be sent to \(q\) from every point in \(OP(q)\). No signal can be sent to \(q\) from any point on the half-curve \(\gamma\).
We are now ready to define the class of models of general relativity which allow for the type of bifurcated supertask mentioned above (Hogarth 1992, 1994).
Definition. A spacetime \((M,g)\) is Malament-Hogarth if there is an event \(q\) in \(M\) and a half-curve \(\gamma\) in \(M\) with infinite elapsed time such that \(\gamma\) is contained in \(OP(q)\).
One can see how the definition corresponds to the story above. Bob travels along the half-curve \(\gamma\) and records an infinite elapsed time. Moreover, at any event on Bob’s worldline, Bob can send a signal to the event \(q\) where Alice finds the result of the computation; this follows from the fact that \(\gamma\) is contained in \(OP(q)\). Note that Alice’s worldline and the starting point \(p\) mentioned in the story did not make it to the definition; they simply weren’t needed. The half curve \(\gamma\) must start at some event – this event is our starting point \(p\). Since \(p\) is in \(OP(q)\), there is a worldline from \(p\) to \(q\). Take this to be Alice’s worldline. One can show that this worldline must have a finite elapsed time.
Is there a spacetime which satisfies the definition? Yes. Let \(M\) be the two-dimensional plane in standard \(t,x\) coordinates. Let the metric \(g\) be such that the light cones are oriented in the \(t\) direction and open up as the absolute value of \(x\) approaches infinity. The resulting spacetime (Anti-de Sitter spacetime) is Malament-Hogarth (see Figure 2.2.2).
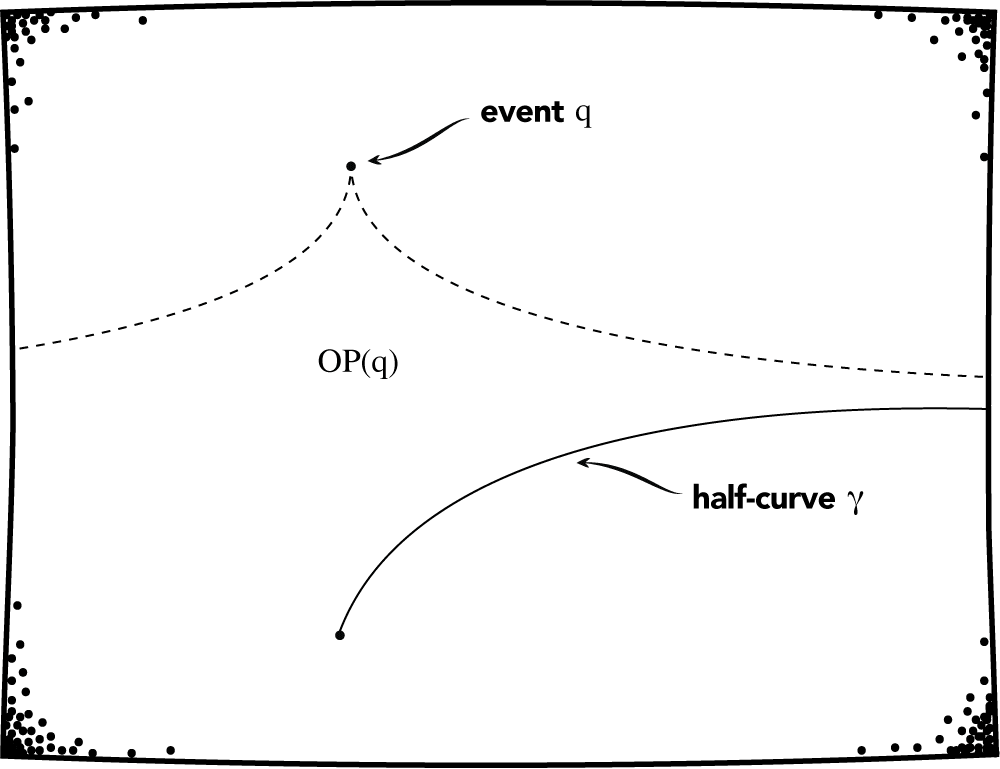
Fig 2.2.2. Anti-de Sitter Spacetime is Malament-Hogarth. A signal can be sent to \(q\) from every point on the half-curve \(\gamma\).
2.3 How Reasonable Are Malament-Hogarth Spacetimes?
In the previous section, we showed the existence of models of general relativity which seem to allow for a type of bifurcated supertask. Here, we ask: Are these models “physically reasonable”? Earman and Norton (1993, 1996) and Etesi and Németi (2002) have articulated a number of potential physical problems concerning Malament-Hogarth spacetimes. First of all, we would like Bob’s worldline to be reasonablly traversable. In the Anti-de Sitter model above, the half-curve \(\gamma\) has an infinite total acceleration. Bob would need an infinite amount of fuel to traverse it! (Malament 1985)
Another problem for the Anti-de Sitter spacetime is that a “divergent blueshift” phenomenon occurs. Intuitively, the frequency of any signal Bob sends to Alice is amplified more and more as he goes along. Eventually, even the slightest thermal noise will be amplified to such an extent that communication is all but impossible. So, if the counterexample to Goldbach’s conjecture comes late in the game (or not at all), it is not clear that Alice can ever know this.
One can find Malament-Hogarth spacetimes which can escape both of the problems mentioned above (Manchak 2010; Andréka et al. 2018). For example, let \(M\) be a two-dimensional plane in standard \(t, x\) coordinates which is then “rolled up” along the \(t\) axis. Let the metric \(g\) be such that the light cones are oriented in the \(t\) direction and do not change from point to point. (See Figure 2.3.1.)
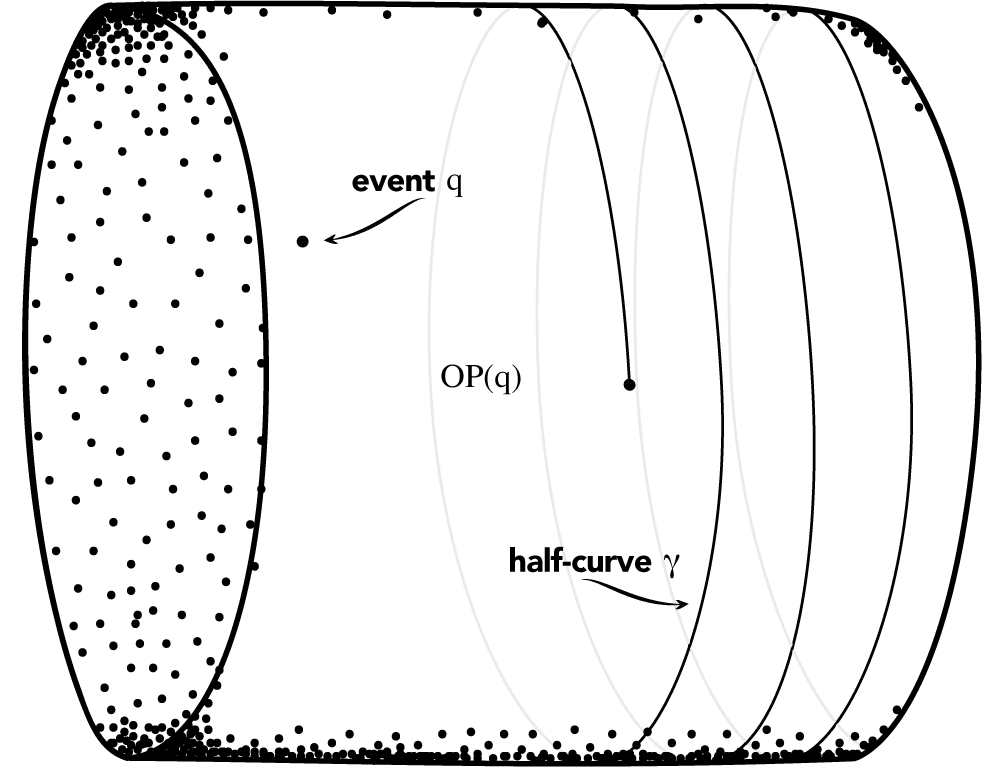
Fig 2.3.1. An acausal Malament-Hogarth spacetime.
Because worldliness can wrap around and around the cylinder, \(OP(q)=M\) for any event \(q\). This allows for great freedom in choosing Bob’s worldline \(\gamma\). In fact, we can choose it so that the total acceleration is zero – no fuel is needed to traverse it. Moreover, we can choose it so that there is also no divergent blueshift phenomenon (see Earman and Norton 1993). But, alas, we have a new problem: the spacetime is acausal. A worldline can start and end at the same event allowing for a type of “time travel”. It is unclear if spacetimes allowing for time travel are physically reasonable (see Smeenk and Wüthrich 2011). It turns out that more complicated examples can be constructed which avoid all the potential problems mentioned so far and more (Manchak 2010). But such examples contain spacetime “holes” which may not be physically reasonable (Manchak 2009; Doboszewski 2019). More work is needed to see if such problems can also be overcome.
We conclude with one final potential problem which threatens to render all Malament-Hogarth spacetimes physically unreasonable. Penrose (1979) has conjectured that all physically reasonable spacetimes are free of a certain type of “naked singularities” and the breakdown of determinism they bring. Whether Penrose’s conjecture is true or not is the subject of much debate (Earman 1995). But it turns out that every Malament-Hogarth spacetime harbors these naked singularities (Hogarth 1992). Even so, the breakdown of determinism guaranteed in such spacetimes does not seem to preclude the construction of Malament-Hogarth “machines” which could possibly bring about supertasks from initial data (Earman et al. 2016; Manchak 2018). Stepping back, we find that it is still an open question whether Malament-Hogarth spacetimes are simply artifact of the formalism of general relativity or if the kind of bifurcated supertask they suggest can be implemented in our own universe.
Bibliography
- Andréka, H., Madarász, J., Németi, I., Németi, P. and G. Székely, 2018, “Relativistic Computation”, in M. Cuffaro and S. Fletcher (eds.), Physical Perspectives on Computation, Computational Perspectives on Physics, Cambridge: Cambridge University Press, 195–215.
- Atkinson, D., 2007, “Losing energy in classical, relativistic and quantum mechanics”, Studies in History and Philosophy of Modern Physics, 38(1): 170–180.
- –––, 2008, “A relativistic zeno effect. Synthese”, 160(1): 5–12.
- Atkinson, D. and Johnson, P., 2009, “Nonconservation of energy and loss of determinism I. Infinitely many colliding balls”, Foundations of Physics, 39(8): 937–957.
- –––, 2010, “Nonconservation of energy and loss of determinism II. Colliding with an open set”, Foundations of Physics, 40(2): 179–189.
- Atkinson, D. and Peijnenburg, J., 2014, “How some infinities cause problems in classical physical theories”, In Allo, P. and Kerkhoeve, B. V., editors, Modestly radical or radically modest: Festschrift for Jean Paul Van Bendegem on the Occasion of his 60th Birthday, pages 1–10. London: College Publications.
- Allis, V. and T. Koetsier, 1991, “On Some Paradoxes of the Infinite”, The British Journal for the Philosophy of Science, 42: 187–194.
- –––, 1995, “On Some Paradoxes of the Infinite II”, The British Journal for the Philosophy of Science, 46: 235–247.
- Barrett, J. A. and F. Arntzenius, 1999, “An infinite decision puzzle”, Theory and Decision, 46(1), 101–103.
- –––, 2002, “Why the infinite decision puzzle is puzzling”, Theory and decision 52(2): 139–147.
- Bashirov, A.E., 2014, Mathematical Analysis Fundamentals Waltham, MA: Elsevier.
- Bell, J. S., 2004, Speakable and unspeakable in quantum mechanics: Collected papers on quantum philosophy. Cambridge: Cambridge University Press.
- Benacerraf, P., 1962, “Tasks, Super-Tasks, and the Modern Eleatics”, The Journal of Philosophy, 59(24): 765–784.
- Benardete, J. A., 1964, Infinity: An essay in metaphysics., Oxford: Oxford University Press.
- Black, M., 1951, “Achilles and the Tortoise”, Analysis, 11(5): 91–101.
- Blum, L., Cucker, F., Shub, M. and Smale, S., 1998, Complexity and real computation, New York: Springer-Verlag.
- Bokulich, A., 2003, “Quantum measurements and supertasks”, International Studies in the Philosophy of Science, 17(2): 127–136.
- Bub, J., 1988, “How to solve the measurement problem of quantum mechanics”, Foundations of Physics 18(7): 701–722.
- Carl, M., Fischbach, T., Koepke, P., Miller, R., Nasfi, M. and Weckbecker, G., 2010, “The basic theory of infinite time register machines”, Archive for Mathematical Logic 49(2): 249–273.
- Copeland, B. J., 2015, “The Church-Turing Thesis”, The Stanford Encyclopedia of Philosophy (Summer 2015 Edition), Edward N. Zalta (ed.), URL = <https://plato.stanford.edu/archives/sum2015/entries/church-turing/>.
- Deolalikar, V., Hamkins, J.D. and Schindler, R., 2005, “P ≠ NP ∩ co-NP for infinite time Turing machines”, Journal of Logic and Computation, 15(5): 577–592.
- Doboszewski, J., 2019, “Epistemic Holes and Determinism in Classical General Relativity”, The British Journal for the Philosophy of Science, 71: 1093–1111. doi:10.1093/bjps/axz011
- Dolev, Y., 2007, “Super-tasks and Temporal Continuity”, Iyyun: The Jerusalem Philosophical Quarterly, 56: 313–329.
- Duncan, A. and M. Niedermaier, 2013, “Temporal breakdown and Borel resummation in the complex Langevin method”, Annals of Physics, 329: 93–124.
- Earman, J., 1986, A Primer On Determinism, Dordrecht, Holland: D. Reidel Publishing Company.
- –––, 1995, Bangs, Crunches, Wimpers, and Shrieks. Oxford University Press.
- Earman, J. and J. Norton, 1993, “Forever is a Day: Supertasks in Pitowsky and Malament-Hogarth Spacetimes”, Philosophy of Science, 60: 22–42.
- –––, 1996, “Infinite Pains: the Trouble with Supertasks”, in A. Morton and S. Stich (eds), Benacerraf and His Critics, Oxford: Blackwell, 231–261.
- Earman, J., Wüthrich, C., and J. Manchak, 2016, “Time Machines”, The Stanford Encyclopedia of Philosophy (Winter 2016 Edition), Edward N. Zalta (ed.), URL = <https://plato.stanford.edu/archives/win2016/entries/time-machine/>.
- Etesi, G. and I. Németi, 2002, “Non-Turing Computations Via Malament-Hogarth Space-Times”, International Journal of Theoretical Physics, 41: 341–370.
- Gamow, G., 1947, One Two Three… Infinity: Facts and Speculations of Science. Dover.
- Ghiradi, G.C., C. Omero, T. Weber and A. Rimini, 1979, “Small-time behaviour of quantum nondecay probability and Zeno’s paradox in quantum mechanics”, Nuovo Cimento, 52(A): 421
- Grünbaum, A., 1969, “Can an Infinitude of Operations be performed in Finite Time?” British Journal for the Philosophy of Science, 20: 203–218.
- Gwiazda, J., 2012, “A proof of the impossibility of completing infinitely many tasks”, Pacific Philosophical Quarterly, 93: 1–7.
- Hamkins, J. D. and Lewis, A., 2000, “Infinite time Turing machines”, Journal of Symbolic Logic, 65(2): 567–604.
- Hamkins, J. D. and Miller, R. G., 2009, “Post’s problem for ordinal register machines: an explicit approach”, Annals of Pure and Applied Logic, 160(3): 302–309.
- Hamkins, J.D., Miller, R., Seabold, D., and Warner, S., 2008, “Infinite time computable model theory”, in New Computational Paradigms: Changing Conceptions of What is Computable, S. B. Cooper, B. Löwe, and A. Sorbi (Eds.), New York: Springer, pgs. 521–557.
- Hamkins, J.D. and Welch, P.D., 2003, “\(P^f \ne NP^f\) for almost all \(f\)”, Mathematical Logic Quarterly, 49(5): 536–540.
- Hepp, K., 1972, “Quantum theory of measurement and macroscopic observables”, Helvetica Physica Acta 45(2): 237–248.
- Hogarth, M., 1992, “Does General Relativity Allow an Observer to View an Eternity in a Finite Time?” Foundations of Physics Letters, 5: 173–181.
- Hogarth, M., 1994, “Non-Turing Computers and Non-Turing Computability”, PSA: Proceedings of the Biennial Meeting of the Philosophy of Science Association, 1: 126–138.
- Immerman, N., 2016, “Computability and Complexity”, The Stanford Encyclopedia of Philosophy (Spring 2016 Edition), Edward N. Zalta (ed.), forthcoming URL = <https://plato.stanford.edu/archives/spr2016/entries/computability/>.
- Koepke, P., 2005, “Turing computations on ordinals” Bulletin of Symbolic Logic, 11(3): 377–397.
- –––, 2006, “Infinite Time Register Machines”, In Logical Approaches to Computational Barriers, Second Conference on Computability in Europe, CiE 2006, Swansea, UK, July 2006, Proceedings, A. Beckmann, U. Berger, B. Löwe, J. V. Tucker (Eds.), Berlin: Springer-Verlag, pgs. 257–266, Lecture Notes in Computer Science 3988.
- –––, 2009, “Ordinal Computability”, In Mathematical Theory and Computational Practice. 5th Conference on Computability in Europe, CiE 2009, Heidelberg, Germany, July 19–24, 2009. Proceedings, K. Ambos-Spies, B. Löwe, W. Merkle (Eds.), Heidelberg: Springer-Verlag, pgs. 280–289, Lecture Notes in Computer Science 5635.
- Koepke, P. and Miller, R., 2008, “An enhanced theory of infinite time register machines”. In Logic and Theory of Algorithms. 4th Conference on Computability in Europe, CiE 2008 Athens, Greece, June 15–20, 2008, Proceedings, Beckmann, A., Dimitracopoulos, C. and Löwe, B. (Eds.), Berlin: Springer, pgs. 306–315, Lecture Notes in Computer Science 5028.
- Koepke, P. and Seyfferth, B., 2009, “Ordinal machines and admissible recursion theory”, Annals of Pure and Applied Logic, 160(3): 310–318.
- Kremer, P., 2015, “The Revision Theory of Truth”, The Stanford Encyclopedia of Philosophy (Summer 2015 Edition), Edward N. Zalta (ed.), URL = <https://plato.stanford.edu/archives/sum2015/entries/truth-revision/>.
- Kühnberger, K.-U., Löwe, B., Möllerfeld, M. and Welch, P.D., 2005, “Comparing inductive and circular definitions: parameters, complexities and games”, Studia Logica, 81: 79–98.
- Landsman, N. P., 1991, “Algebraic theory of superselection sectors and the measurement problem in quantum mechanics”, International Journal of Modern Physics A 6(30): 5349–5371.
- –––, 1995, “Observation and superselection in quantum mechanics”, Studies in History and Philosophy of Modern Physics, 26(1): 45–73.
- Lanford, O. E. (1975) “Time Evolution of Large Classical Systems”, in Dynamical systems, theory and applications, J. Moser (Ed.), Springer Berlin Heidelberg, pgs. 1–111.
- Littlewood, J. E., 1953, A Mathematician’s Miscellany, London: Methuen & Co. Ltd.
- Löwe, B., 2001, “Revision sequences and computers with an infinite amount of time”, Journal of Logic and Computation, 11: 25–40.
- –––, 2006, “Space bounds for infinitary computation”, in Logical Approaches to Computational Barriers, Second Conference on Computability in Europe, CiE 2006, Swansea, UK, July 2006, Proceedings, A. Beckmann, U. Berger, B. Löwe, J. V. Tucker (eds.), Berlin: Springer-Verlag, pgs. 319–329, Lecture Notes in Computer Science 3988.
- Löwe, B. and Welch, P. D., 2001, “Set-Theoretic Absoluteness and the Revision Theory of Truth”, Studia Logica, 68: 21–41.
- Mather, J. N. and R. McGehee, 1975, “Solutions of the Collinear Four-Body Problem Which Become Unbounded in a Finite Time”, in Dynamical systems, theory and applications, J. Moser (Ed.), Springer Berlin Heidelberg, pgs. 573–597.
- Misra, B., and E. C. G. Sudarshan, 1977, “The Zeno’s paradox in quantum theory”, Journal of Mathematical Physics, 18(4): 756–763.
- Malament, D., 1985, “Minimal Acceleration Requirements for ”Time Travel“ in Gödel Space-Time”, Journal of Mathematical Physics, 26: 774–777.
- –––, 2008, “Norton’s Slippery Slope”, Philosophy of Science, 75: 799–816.
- Manchak, J., 2009, “Is Spacetime Hole-Free?” General Relativity and Gravitation, 41: 1639–1643.
- –––, 2010, “On the Possibility of Supertasks in General Relativity”, Foundations of Physics, 40: 276–288.
- –––, 2018, “Malament-Hogarth Machines”, The British Journal for the Philosophy of Science, 71: 1143–1153. doi:10.1093/bjps/axy023
- Mclaughlin, William I., 1998, “Thomson’s lamp is dysfunctional”, Synthese, 116: 281–301.
- Norton, J. D., 1999, “A Quantum Mechanical Supertask”, Foundations of Physics, 29(8): 1265–1302.
- Penrose, R., 1979, “Singularities and Time-Asymmetry”, in S. Hawking and W. Israel (eds.), General Relativity: And Einstein Centenary Survey, Cambridge: Cambridge University Press, 581–638.
- Pati, A. K., 1996, “Limit on the frequency of measurements in the quantum Zeno effect”, Physics Letters A 215(1–2): 7–13.
- Peijnenburg, J. and Atkinson, D., 2008, “Achilles, the tortoise, and colliding balls”, History of Philosophy Quarterly, 25(3): 187–201.
- Pérez Laraudogoita, J., 1996, “A beautiful supertask”, Mind, 105(417): 81–83.
- –––, 1997, “Classical particle dynamics, indeterminism and a supertask”, The British Journal for the Philosophy of Science, 48(1): 49–54.
- –––, 1998, “Infinity Machines and Creation Ex Nihilo”, Synthese, 115(2): 259–265.
- –––, 1999, “Earman and Norton on Supertasks that Generate Indeterminism”, The British Journal for the Philosophy of Science, 50: 137–141.
- Pérez Laraudogoita, J., M. Bridger and J. S. Alper, 2002, “Two Ways Of Looking At A Newtonian Supertask”, Synthese, 131(2): 173–189
- Pitowsky, I., 1990, “The Physical Church Thesis and Physical Computational Complexity”, Iyyun, 39: 81–99.
- Rin, B., 2014, “The Computational Strengths of α-tape Infinite Time Turing Machines”, Annals of Pure and Applied Logic, 165(9): 1501–1511.
- Ross, S. E., 1976, A First Course in Probability, Macmillan Publishing Co. Inc.
- Sacks, G. E., 1990, Higher recursion theory, Heidelberg: Springer-Verlag, Perspectives in mathematical logic.
- Salmon, W., 1998, “A Contemporary Look at Zeno’s Paradoxes: An Excerpt from Space, Time and Motion”, in Metaphysics: The Big Questions, van Inwagen and Zimmerman (Eds.), Malden, MA: Blackwell Publishers Ltd.
- Schindler, R., 2003, “P ≠ NP for infinite time Turing machines”, Monatshefte der Mathematik 139(4): 335–340.
- Smeenk, C. and C. Wüthrich, 2011, “Time Travel and Time Machines”, in C. Callender (ed.), The Oxford Handbook of Philosophy of Time, Oxford: Oxford University Press, 577–630.
- Thomson, J. F., 1954, “Tasks and super-tasks”, Analysis, 15(1): 1–13.
- Uzquiano, G., 2011, “Before-Effect without Zeno-Causality” Noûs, 46(2): 259–264.
- Van Bendegem, J. P., 1994, “Ross’ Paradox Is an Impossible Super-Task”, The British Journal for the Philosophy of Science, 45(2): 743–748.
- Wan, K-K., 1980, “Superselection rules, quantum measurement, and the Schrödinger’s cat”, Canadian Journal of Physics, 58(7): 976–982.
- Welch, P. D. 2001, “On Gupta-Belnap revision theories of truth, Kripkean fixed points, and the Next stable set”, Bulletin for Symbolic Logic, 7: 345–360.
- –––, 2008, “The extent of computation in Malament-Hogarth spacetimes”, British Journal for the Philosophy of Science, 59(4): 659–674.
- Weyl, H., 1949, Philosophy of Mathematics and Natural Science, Princeton: Princeton University Press.
- Winter, J., 2009, “Is \(\mathbf{P} = \mathbf{PSPACE}\) for Infinite Time Turing Machines?”, in Infinity in logic and computation. Revised selected papers from the International Conference (ILC 2007) held at the University of Cape Town (UCT), Cape Town, November 3–5, 2007. M. Archibald, V. Brattka, V. Goranko and B. Löwe (Eds.), Berlin: Springer-Verlag, pgs. 126–137. Lecture Notes in Computer Science 5489.
Academic Tools
How to cite this entry. Preview the PDF version of this entry at the Friends of the SEP Society. Look up topics and thinkers related to this entry at the Internet Philosophy Ontology Project (InPhO). Enhanced bibliography for this entry at PhilPapers, with links to its database.
Other Internet Resources
- Malament, D., 2009, “Note on Carnap’s ‘On the Dependence of the Properties of Space Upon Those of Time’”, unpublished manuscript, PhilSci-Archive.
- Laraudogoitia, Jon Pérez, “Supertasks,” Stanford Encyclopedia of Philosophy (Spring 2016 Edition), Edward N. Zalta (ed.), URL = <https://plato.stanford.edu/archives/spr2016/entries/spacetime-supertasks/>. [This was the previous entry on supertasks in the Stanford Encyclopedia of Philosophy — see the version history.]


