Quantum Mechanics
Quantum mechanics is, at least at first glance and at least in part, a mathematical machine for predicting the behaviors of microscopic particles — or, at least, of the measuring instruments we use to explore those behaviors — and in that capacity, it is spectacularly successful: in terms of power and precision, head and shoulders above any theory we have ever had. Mathematically, the theory is well understood; we know what its parts are, how they are put together, and why, in the mechanical sense (i.e., in a sense that can be answered by describing the internal grinding of gear against gear), the whole thing performs the way it does, how the information that gets fed in at one end is converted into what comes out the other. The question of what kind of a world it describes, however, is controversial; there is very little agreement, among physicists and among philosophers, about what the world is like according to quantum mechanics. Minimally interpreted, the theory describes a set of facts about the way the microscopic world impinges on the macroscopic one, how it affects our measuring instruments, described in everyday language or the language of classical mechanics. Disagreement centers on the question of what a microscopic world, which affects our apparatuses in the prescribed manner, is, or even could be, like intrinsically; or how those apparatuses could themselves be built out of microscopic parts of the sort the theory describes.[1]
That is what an interpretation of the theory would provide: a proper account of what the world is like according to quantum mechanics, intrinsically and from the bottom up. The problems with giving an interpretation (not just a comforting, homey sort of interpretation, i.e., not just an interpretation according to which the world isn’t too different from the familiar world of common sense, but any interpretation at all) are dealt with in other sections of this encyclopedia. Here, we are concerned only with the mathematical heart of the theory, the theory in its capacity as a mathematical machine, and — whatever is true of the rest of it — this part of the theory makes exquisitely good sense.
- 1. Terminology
- 2. Mathematics
- 3. Quantum Mechanics
- 4. Structures on Hilbert Space
- Bibliography
- Academic Tools
- Other Internet Resources
- Related Entries
1. Terminology
Physical systems are divided into types according to their unchanging (or ‘state-independent’) properties, and the state of a system at a time consists of a complete specification of those of its properties that change with time (its ‘state-dependent’ properties). To give a complete description of a system, then, we need to say what type of system it is and what its state is at each moment in its history.
A physical quantity is a mutually exclusive and jointly exhaustive family of physical properties (for those who know this way of talking, it is a family of properties with the structure of the cells in a partition). Knowing what kinds of values a quantity takes can tell us a great deal about the relations among the properties of which it is composed. The values of a bivalent quantity, for instance, form a set with two members; the values of a real-valued quantity form a set with the structure of the real numbers. This is a special case of something we will see again and again, viz., that knowing what kind of mathematical objects represent the elements in some set (here, the values of a physical quantity; later, the states that a system can assume, or the quantities pertaining to it) tells us a very great deal (indeed, arguably, all there is to know) about the relations among them.
In quantum mechanical contexts, the term ‘observable’ is used interchangeably with ‘physical quantity’, and should be treated as a technical term with the same meaning. It is no accident that the early developers of the theory chose the term, but the choice was made for reasons that are not, nowadays, generally accepted. The state-space of a system is the space formed by the set of its possible states,[2] i.e., the physically possible ways of combining the values of quantities that characterize it internally. In classical theories, a set of quantities which forms a supervenience basis for the rest is typically designated as ‘basic’ or ‘fundamental’, and, since any mathematically possible way of combining their values is a physical possibility, the state-space can be obtained by simply taking these as coordinates.[3] So, for instance, the state-space of a classical mechanical system composed of \(n\) particles, obtained by specifying the values of \(6n\) real-valued quantities — three components of position, and three of momentum for each particle in the system — is a \(6n\)-dimensional coordinate space. Each possible state of such a system corresponds to a point in the space, and each point in the space corresponds to a possible state of such a system. The situation is a little different in quantum mechanics, where there are mathematically describable ways of combining the values of the quantities that don’t represent physically possible states. As we will see, the state-spaces of quantum mechanics are special kinds of vector spaces, known as Hilbert spaces, and they have more internal structure than their classical counterparts.
A structure is a set of elements on which certain operations and relations are defined, a mathematical structure is just a structure in which the elements are mathematical objects (numbers, sets, vectors) and the operations mathematical ones, and a model is a mathematical structure used to represent some physically significant structure in the world.
The heart and soul of quantum mechanics is contained in the Hilbert spaces that represent the state-spaces of quantum mechanical systems. The internal relations among states and quantities, and everything this entails about the ways quantum mechanical systems behave, are all woven into the structure of these spaces, embodied in the relations among the mathematical objects which represent them.[4] This means that understanding what a system is like according to quantum mechanics is inseparable from familiarity with the internal structure of those spaces. Know your way around Hilbert space, and become familiar with the dynamical laws that describe the paths that vectors travel through it, and you know everything there is to know, in the terms provided by the theory, about the systems that it describes.
By ‘know your way around’ Hilbert space, I mean something more than possess a description or a map of it; anybody who has a quantum mechanics textbook on their shelf has that. I mean know your way around it in the way you know your way around the city in which you live. This is a practical kind of knowledge that comes in degrees and it is best acquired by learning to solve problems of the form: How do I get from A to B? Can I get there without passing through C? And what is the shortest route? Graduate students in physics spend long years gaining familiarity with the nooks and crannies of Hilbert space, locating familiar landmarks, treading its beaten paths, learning where secret passages and dead ends lie, and developing a sense of the overall lay of the land. They learn how to navigate Hilbert space in the way a cab driver learns to navigate his city.
How much of this kind of knowledge is needed to approach the philosophical problems associated with the theory? In the beginning, not very much: just the most general facts about the geometry of the landscape (which is, in any case, unlike that of most cities, beautifully organized), and the paths that (the vectors representing the states of) systems travel through them. That is what will be introduced here: first a bit of easy math, and then, in a nutshell, the theory.
2. Mathematics
2.1 Vectors and vector spaces
A vector \(A\), written ‘\(\ket{A}\)’, is a mathematical object characterized by a length, \(|A|\), and a direction. A normalized vector is a vector of length 1; i.e., \(|A| = 1\). Vectors can be added together, multiplied by constants (including complex numbers), and multiplied together. Vector addition maps any pair of vectors onto another vector, specifically, the one you get by moving the second vector so that its tail coincides with the tip of the first, without altering the length or direction of either, and then joining the tail of the first to the tip of the second. This addition rule is known as the parallelogram law. So, for example, adding vectors \(\ket{A}\) and \(\ket{B}\) yields vector \(\ket{C} (= \ket{A} + \ket{B})\) as in Figure 1:
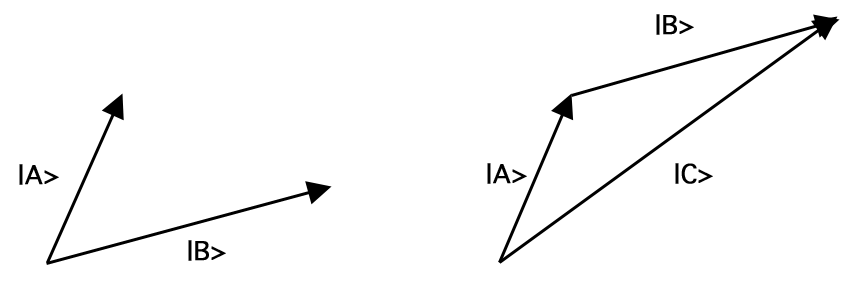
Figure 1. Vector Addition
Multiplying a vector \(\ket{A}\) by \(n\), where \(n\) is a constant, gives a vector which is the same direction as \(\ket{A}\) but whose length is \(n\) times \(\ket{A}\)’s length.
In a real vector space, the (inner or dot) product of a pair of vectors \(\ket{A}\) and \(\ket{B}\), written ‘\(\braket{A}{B}\)’ is a scalar equal to the product of their lengths (or ‘norms’) times the cosine of the angle, \(\theta\), between them:
\[ \braket{A}{B} = |A| |B| \cos \theta \]Let \(\ket{A_1}\) and \(\ket{A_2}\) be vectors of length 1 (“unit vectors”) such that \(\braket{A_1}{A_2} = 0\). (So the angle between these two unit vectors must be 90 degrees.) Then we can represent any two-dimensional vector \(\ket{B}\) in terms of our unit vectors as follows:
\[ \ket{B} = b_1 \ket{A_1} + b_2 \ket{A_2} \]For example, here is a graph which shows how \(\ket{B}\) can be represented as the sum of the two unit vectors \(\ket{A_1}\) and \(\ket{A_2}\):
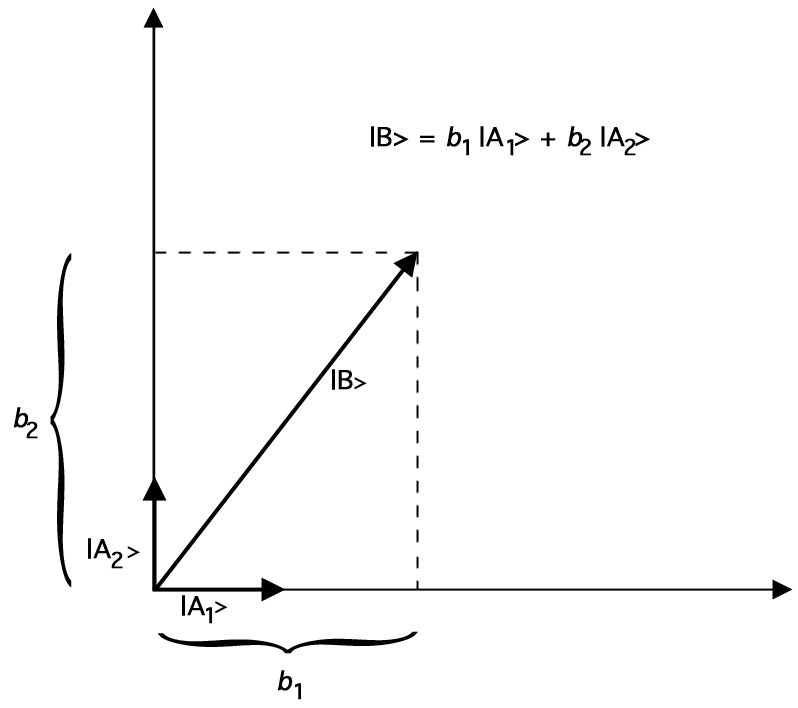
Figure 2. Representing \(\ket{B}\) by Vector Addition of Unit Vectors
Now the definition of the inner product \(\braket{A}{B}\) has to be modified to apply to complex spaces. Let \(c^*\) be the complex conjugate of \(c\). (When \(c\) is a complex number of the form \(a \pm bi\), then the complex conjugate \(c^*\) of \(c\) is defined as follows:
\[ [a+bi]^* = a-bi \\ [a-bi]^* = a+bi \]So, for all complex numbers \(c\), \([c^*]^* = c\), but \(c^* = c\) just in case \(c\) is real.) Now definition of the inner product of \(\ket{A}\) and \(\ket{B}\) for complex spaces can be given in terms of the conjugates of complex coefficients as follows. Where \(\ket{A_1}\) and \(\ket{A_2}\) are the unit vectors described earlier, \(\ket{A} = a_1 \ket{A_1} + a_2 \ket{A_2}\) and \(\ket{B} = b_1 \ket{A_1} + b_2 \ket{A_2}\), then
\[ \braket{A}{B} = (a_1^*)(b_1) + (a_2^*)(b_2) \]The most general and abstract notion of an inner product, of which we’ve now defined two special cases, is as follows. \(\braket{A}{B}\) is an inner product on a vector space \(V\) just in case
- \(\braket{A}{A} = |A|^2\), and \(\braket{A}{A}=0\) if and only if \(A=0\)
- \(\braket{B}{A} = \braket{A}{B}^*\)
- \(\braket{B}{A+C}=\braket{B}{A} + \braket{B}{C}\).
It follows from this that
- the length of \(\ket{A}\) is the square root of inner product of \(\ket{A}\) with itself, i.e., \[ |A| = \sqrt{\braket{A}{A}} \]
and
- \(\ket{A}\) and \(\ket{B}\) are mutually perpendicular, or orthogonal, if, and only if, \(\braket{A}{B} = 0\).
A vector space is a set of vectors closed under addition, and multiplication by constants, an inner product space is a vector space on which the operation of vector multiplication has been defined, and the dimension of such a space is the maximum number of nonzero, mutually orthogonal vectors it contains.
Any collection of \(N\) mutually orthogonal vectors of length 1 in an \(N\)-dimensional vector space constitutes an orthonormal basis for that space. Let \(\ket{A_1}, \ldots, \ket{A_N}\) be such a collection of unit vectors. Then every vector in the space can be expressed as a sum of the form:
\[ \ket{B} = b_1 \ket{A_1} + b_2 \ket{A_2} + \ldots + b_N \ket{A_N}, \]where \(b_i = \braket{B}{A_i}\). The \(b_i\)’s here are known as \(B\)’s expansion coefficients in the \(A\)-basis.[5]
Notice that:
- for all vectors \(A\), \(B\), and \(C\) in a given space, \[ \braket{A}{B+C} = \braket{A}{B} + \braket{A}{C} \]
- for any vectors \(M\) and \(Q\), expressed in terms of the
\(A\)-basis,
\[ \ket{M} + \ket{Q} = \sum_{i=1}^N (m_i + q_i) \ket{A_i}, \]
and
\[ \braket{M}{Q} = \sum_{i=1}^N m_i^* q_i \]
There is another way of writing vectors, namely by writing their expansion coefficients (relative to a given basis) in a column, like so:
\[ \ket{Q} = \begin{bmatrix} q_1 \\ q_2 \end{bmatrix} \]where \(q_i = \braket{Q}{A_i}\) and the \(A_i\) are the chosen basis vectors.
When we are dealing with vector spaces of infinite dimension, since we can’t write the whole column of expansion coefficients needed to pick out a vector since it would have to be infinitely long, so instead we write down the function (called the ‘wave function’ for \(Q\), usually represented \(\psi(i))\) which has those coefficients as values. We write down, that is, the function:
\[ \psi(i) = q_i = \braket{Q}{A_i} \]Given any vector in, and any basis for, a vector space, we can obtain the wave-function of the vector in that basis; and given a wave-function for a vector, in a particular basis, we can construct the vector whose wave-function it is. Since it turns out that most of the important operations on vectors correspond to simple algebraic operations on their wave-functions, this is the usual way to represent state-vectors.
When a pair of physical systems interact, they form a composite system, and, in quantum mechanics as in classical mechanics, there is a rule for constructing the state-space of a composite system from those of its components, a rule that tells us how to obtain, from the state-spaces, \(H_A\) and \(H_B\) for \(A\) and \(B\), respectively, the state-space — called the ‘tensor product’ of \(H_A\) and \(H_B\), and written \(H_A \otimes H_B\) — of the pair. There are two important things about the rule; first, so long as \(H_A\) and \(H_B\) are Hilbert spaces, \(H_A \otimes H_B\) will be as well, and second, there are some facts about the way \(H_A \otimes H_B\) relates to \(H_A\) and \(H_B\), that have surprising consequences for the relations between the complex system and its parts. In particular, it turns out that the state of a composite system is not uniquely defined by those of its components. What this means, or at least what it appears to mean, is that there are, according to quantum mechanics, facts about composite systems (and not just facts about their spatial configuration) that don’t supervene on facts about their components; it means that there are facts about systems as wholes that don’t supervene on facts about their parts and the way those parts are arranged in space. The significance of this feature of the theory cannot be overplayed; it is, in one way or another, implicated in most of its most difficult problems.
In a little more detail: if \(\{v_{i}^A\}\) is an orthonormal basis for \(H_A\) and \(\{u_{j}^B\}\) is an orthonormal basis for \(H_B\), then the set of pairs \((v_{i}^A, u_{j}^B)\) is taken to form an orthonormal basis for the tensor product space \(H_A \otimes H_B\). The notation \(v_i^A \otimes u_j^B\) is used for the pair \((v_{i}^A,u_{j}^B)\), and inner product on \(H_A \otimes H_B\) is defined as:[6]
\[ \braket{v_i^A \otimes u_m^B}{v_j^A \otimes u_n^B} = \braket{v_i^A}{v_j^A} \braket{u_m^B}{u_n^B} \]It is a result of this construction that although every vector in \(H_A \otimes H_B\) is a linear sum of vectors expressible in the form \(v^A \otimes u^B\), not every vector in the space is itself expressible in that form, and it turns out that
- any composite state defines uniquely the states of its components.
- if the states of \(A\) and \(B\) are pure (i.e., representable by vectors \(v^A\) and \(u^B\), respectively), then the state of \((A+B)\) is pure and represented by \(v^A \otimes u^B\), and
- if the state of \((A+B)\) is pure and expressible in the form \(v^A \otimes u^B\), then the states of \(A\) and \(B\) are pure, but
- if the states of \(A\) and \(B\) are not pure, i.e., if they are mixed states (these are defined below), they do not uniquely define the state of \((A+B)\); in particular, it may be a pure state not expressible in the form \(v^A \otimes u^B\).
2.2 Operators
An operator \(O\) is a mapping of a vector space onto itself; it takes any vector \(\ket{B}\) in a space onto another vector \(\ket{B'}\) also in the space; \(O \ket{B} = \ket{B'}\). Linear operators are operators that have the following properties:
- \(O(\ket{A} + \ket{B}) = O \ket{A} + O \ket{B}\), and
- \(O(c \ket{A}) = c(O \ket{A})\).
Just as any vector in an \(N\)-dimensional space can be represented by a column of \(N\) numbers, relative to a choice of basis for the space, any linear operator on the space can be represented in a column notation by \(N^2\) numbers:
\[O = \begin{bmatrix} O_{11} & O_{12} \\ O_{21} & O_{22} \end{bmatrix}\]where \(O_{ij} = \braket{A_i}{O \mid A_j}\) and the \(A_N\) are the basis vectors of the space. The effect of the linear operator \(O\) on the vector \(B\) is, then, given by
\[\begin{align} O \ket{B} &= \begin{bmatrix} O_{11} & O_{12} \\ O_{21} & O_{22} \end{bmatrix} \times \begin{bmatrix} b_1 \\ b_2 \end{bmatrix} \\ &= \begin{bmatrix} (O_{11}b_1 + O_{12}b_2) \\ (O_{21}b_1 + O_{22}b_2) \end{bmatrix} \\ &= (O_{11}b_1 + O_{12}b_2)|A_1\rangle + (O_{21}b_1 + O_{22}b_2|A_2\rangle \\ &=|B'\rangle \end{align}\]Two more definitions before we can say what Hilbert spaces are, and then we can turn to quantum mechanics. \(\ket{B}\) is an eigenvector of \(O\) with eigenvalue \(a\) if, and only if, \(O \ket{B} = a \ket{B}\). Different operators can have different eigenvectors, but the eigenvector/operator relation depends only on the operator and vectors in question, and not on the particular basis in which they are expressed; the eigenvector/operator relation is, that is to say, invariant under change of basis. A Hermitean operator is an operator which has the property that there is an orthonormal basis consisting of its eigenvectors and those eigenvalues are all real.
A Hilbert space, finally, is a vector space on which an inner product is defined, and which is complete, i.e., which is such that any Cauchy sequence of vectors in the space converges to a vector in the space. All finite-dimensional inner product spaces are complete, and I will restrict myself to these. The infinite case involves some complications that are not fruitfully entered into at this stage.
3. Quantum Mechanics
Four basic principles of quantum mechanics are:
- (3.1)
-
Physical States. Every physical system is associated with a Hilbert Space, every unit vector in the space corresponds to a possible pure state of the system, and every possible pure state, to some vector in the space.[7]
- (3.2)
-
Physical Quantities. Hermitian operators in the Hilbert space associated with a system represent physical quantities, and their eigenvalues represent the possible results of measurements of those quantities.
There is an operator, called the Hamiltonian, that plays a special role in quantum theory because the dynamics of a system can be conveniently formulated by tracking its evolution. The Hamiltonian – written \(H\), or \(\hat{H}\) – stands for the total energy of the system. Its eigenvalues are the possible results that might be obtained in measurements of total energy. It is given by summing over the kinetic and potential energies of the system’s components.
- (3.3)
-
Composition. The Hilbert space associated with a complex system is the tensor product of those associated with the simple systems (in the standard, non-relativistic, theory: the individual particles) of which it is composed.
- (3.4)
- Dynamics.
- a.
-
Contexts of type 1: Given the state of a system at \(t\) and the forces and constraints to which it is subject, there is an equation, ‘Schrödinger’s equation’, that gives the state at any other time \(U \ket{v_t} \rightarrow \ket{v_{t'}}\).[8] The important properties of \(U\) for our purposes are that it is deterministic, which is to say that it takes the state of a system at one time into a unique state at any other, it is unitary, which means that it is an automorphism of the Hilbert space on which it acts (i.e., a mapping of that space onto itself that preserves the linear space structure and inner product), and it is linear, which is to say that if it takes a state \(\ket{A}\) onto the state \(\ket{A'}\), and it takes the state \(\ket{B}\) onto the state \(\ket{B'}\), then it takes any state of the form \(\alpha \ket{A} + \beta \ket{B}\) onto the state \(\alpha \ket{A'} + \beta \ket{B'}\).
- b.
-
Contexts of type 2 (“Measurement Contexts”):[9] Carrying out a “measurement” of an observable \(B\) on a system in a state \(\ket{A}\) has the effect of collapsing the system into a \(B\)-eigenstate corresponding to the eigenvalue observed. This is known as the Collapse Postulate. Which particular \(B\)-eigenstate it collapses into is a matter of probability, and the probabilities are given by a rule known as Born’s Rule:
\[ \Pr(b_i) = |\braket{A}{B=b_i}|^2 \]
There are two important points to note about these two kinds of contexts:
- The distinction between contexts of type 1 and 2 remains to be made out in quantum mechanical terms; nobody has managed to say in a completely satisfactory way, in the terms provided by the theory, which contexts are measurement contexts, and
- Even if the distinction is made out, it is an open interpretive question whether there are contexts of type 2; i.e., it is an open interpretive question whether there are any contexts in which systems are governed by a dynamical rule other than Schrödinger’s equation.
4. Structures on Hilbert Space
I remarked above that in the same way that all the information we have about the relations between locations in a city is embodied in the spatial relations between the points on a map which represent them, all of the information that we have about the internal relations among (and between) states and quantities in quantum mechanics is embodied in the mathematical relations among the vectors and operators which represent them.[10] From a mathematical point of view, what really distinguishes quantum mechanics from its classical predecessors is that states and quantities have a richer structure; they form families with a more interesting network of relations among their members.
All of the physically consequential features of the behaviors of quantum mechanical systems are consequences of mathematical properties of those relations, and the most important of them are easily summarized:
- (P1)
-
Any way of adding vectors in a Hilbert space or multiplying them by scalars will yield a vector that is also in the space. In the case that the vector is normalized, it will, from (3.1), represent a possible state of the system, and in the event that it is the sum of a pair of eigenvectors of an observable \(B\) with distinct eigenvalues, it will not itself be an eigenvector of \(B\), but will be associated, from (3.4b), with a set of probabilities for showing one or another result in \(B\)-measurements.
- (P2)
-
For any Hermitian operator on a Hilbert space, there are others, on the same space, with which it doesn’t share a full set of eigenvectors; indeed, it is easy to show that there are other such operators with which it has no eigenvectors in common.
If we make a couple of additional interpretive assumptions, we can say more. Assume, for instance, that
- (4.1)
-
Every Hermitian operator on the Hilbert space associated with a system represents a distinct observable, and (hence) every normalized vector, a distinct state, and
- (4.2)
-
A system has a value for observable \(A\) if, and only if, the vector representing its state is an eigenstate of the \(A\)-operator. The value it has, in such a case, is just the eigenvalue associated with that eigenstate.[11]
It follows from (P2), by (3.1), that no quantum mechanical state is an eigenstate of all observables (and indeed that there are observables which have no eigenstates in common), and so, by (3.2), that no quantum mechanical system ever has simultaneous values for all of the quantities pertaining to it (and indeed that there are pairs of quantities to which no state assigns simultaneous values).
There are Hermitian operators on the tensor product \(H_1 \otimes H_2\) of a pair of Hilbert spaces \(H_1\) and \(H_2\) ... In the event that \(H_1\) and \(H_2\) are the state spaces of systems \(S1\) and \(S2\), \(H_1 \otimes H_2\) is the state-space of the complex system \((S1+S2)\). It follows from this by (4.1) that there are observables pertaining to \((S1+S2)\) whose values are not determined by the values of observables pertaining to the two individually.
These are all straightforward consequences of taking vectors and operators in Hilbert space to represent, respectively, states and observables, and applying Born’s Rule (and later (4.1) and (4.2)), to give empirical meaning to state assignments. That much is perfectly well understood; the real difficulty in understanding quantum mechanics lies in coming to grips with their implications — physical, metaphysical, and epistemological.
Anyone trying to come to an understanding about what quantum mechanics says about the world has to grapple with one remaining fact. This problem is not an issue with Hilbert spaces, but of the dynamics – the rules that describe the trajectories that systems follow through the space. From a physical point of view, it is far more worrisome than anything discussed to this point. It not only presents difficulties to someone trying to provide an interpretation of the theory, but also seems to point to a logical inconsistency in the theory’s foundations.
Suppose that we have a system \(S\) and a device \(S^*\) which measures an observable \(A\) on \(S\) with values \(\{a_1, a_2, a_3, ...\}\). Then there is some state of \(S^*\) (the ‘ground state’), and some observable \(B\) with values \(\{b_1, b_2, b_3, ...\}\) pertaining to \(S^*\) (its ‘pointer observable’, so called because it is whatever plays the role of the pointer on a dial on the front of a schematic measuring instrument in registering the result of the experiment), which are such that, if \(S^*\) is started in its ground state and interacts in an appropriate way with \(S\), and if the value of \(A\) immediately before the interaction is \(a_1\), then \(B\)’s value immediately thereafter is \(b_1\). If, however, \(A\)’s value immediately before the interaction is \(a_2\), then \(B\)’s value afterwards is \(b_2\); if the value of \(A\) immediately before the interaction is \(a_3\), then \(B\)’s value immediately after is \(b_3\), and so on. That is just what it means to say that \(S^*\) measures \(A\). So, if we represent the joint, partial state of \(S\) and \(S^*\) (just the part of it which specifies the value of [\(A\) on \(S\) & \(B\) on \(S^*\)], the observable whose values correspond to joint assignments of values to the measured observable on \(S\) and the pointer observable on \(S^*\)) by the vector \(\ket{A=a_i}_s \ket{B=b_i}_{s^*}\), and let “\(\rightarrow\)” stand in for the dynamical description of the interaction between the two, to say that \(S^*\) is a measuring instrument for \(A\) is to say that the dynamical laws entail that,
\[\begin{align} \ket{A=a_1}_s \ket{B=\text{ground state}}_{s^*} &\rightarrow \ket{A=a_1}_s \ket{B=b_1}_{s^*} \\ \ket{A=a_2}_s \ket{B=\text{ground state}}_{s^*} &\rightarrow \ket{A=a_2}_s \ket{B=b_2}_{s^*} \\ \ket{A=a_3}_s \ket{B=\text{ground state}}_{s^*} &\rightarrow \ket{A=a_3}_s \ket{B=b_3}_{s^*} \end{align}\]and so on.[12]
Intuitively, \(S^*\) is a measuring instrument for an observable \(A\) just in case there is some observable feature of \(S^*\) (it doesn’t matter what, just something whose values can be ascertained by looking at the device), which is correlated with the \(A\)-values of systems fed into it in such a way that we can read those values off of \(S^*\)’s observable state after the interaction. In philosophical parlance, \(S^*\) is a measuring instrument for \(A\) just in case there is some observable feature of \(S^*\) which tracks or indicates the \(A\)-values of systems with which it interacts in an appropriate way.
Now, it follows from (3.1), above, that there are states of \(S\) (too many to count) which are not eigenstates of \(A\), and if we consider what Schrödinger’s equation tells us about the joint evolution of \(S\) and \(S^*\) when \(S\) is started out in one of these, we find that the state of the pair after interaction is a superposition of eigenstates of [\(A\) on \(S\) & \(B\) on \(S^*\)]. It doesn’t matter what observable on \(S\) is being measured, and it doesn’t matter what particular superposition \(S\) starts out in; when it is fed into a measuring instrument for that observable, if the interaction is correctly described by Schrödinger’s equation, it follows just from the linearity of the \(U\) in that equation, the operator that effects the transformation from the earlier to the later state of the pair, that the joint state of \(S\) and the apparatus after the interaction is a superposition of eigenstates of this observable on the joint system.
Suppose, for example, that we start \(S^*\) in its ground state, and \(S\) in the state
\[ \frac{1}{\sqrt{2}} \ket{A = a_1}_s + \frac{1}{\sqrt{2}} \ket{A=a_2}_s \]It is a consequence of the rules for obtaining the state-space of the composite system that the combined state of the pair is
\[ \frac{1}{\sqrt{2}} \ket{A=a_1}_s \ket{B=\text{ground state}}_{s^*} + \frac{1}{\sqrt{2}} \ket{A = a_2}_s \ket{B = \text{ground state}}_{s^*} \]and it follows from the fact that \(S^*\) is a measuring instrument for \(A\), and the linearity of \(U\) that their combined state after interaction, is
\[ \frac{1}{\sqrt{2}} \ket{A=a_1}_s \ket{B=b_1}_{s^*} + \frac{1}{\sqrt{2}} \ket{A = a_2}_s \ket{B = b_2}_{s^*} \]This, however, is inconsistent with the dynamical rule for contexts of type 2, for the dynamical rule for contexts of type 2 (and if there are any such contexts, this is one) entails that the state of the pair after interaction is either
\[ \ket{A=a_1}_s \ket{B=b_1}_{s^*} \]or
\[ \ket{A=a_2}_s \ket{B=b_2}_{s^*} \]Indeed, it entails that there is a precise probability of \(\frac{1}{2}\) that it will end up in the former, and a probability of \(\frac{1}{2}\) that it will end up in the latter.
We can try to restore logical consistency by giving up the dynamical rule for contexts of type 2 (or, what amounts to the same thing, by denying that there are any such contexts), but then we have the problem of consistency with experience. For it was no mere blunder that that rule was included in the theory; we know what a system looks like when it is in an eigenstate of a given observable, and we know from looking that the measuring apparatus after measurement is in an eigenstate of the pointer observable. And so we know from the outset that if a theory tells us something else about the post-measurement states of measuring apparatuses, whatever that something else is, it is wrong.
That, in a nutshell, is the Measurement Problem in quantum mechanics; any interpretation of the theory, any detailed story about what the world is like according to quantum mechanics, and in particular those bits of the world in which measurements are going on, has to grapple with it.
Loose Ends
Mixed states are weighted sums of pure states, and they can be used to represent the states of ensembles whose components are in different pure states, or states of individual systems about which we have only partial knowledge. In the first case, the weight attached to a given pure state reflects the size of the component of the ensemble which is in that state (and hence the objective probability that an arbitrary member of the ensemble is); in the second case, they reflect the epistemic probability that the system in question to which the state is assigned is in that state.If we don’t want to lose the distinction between pure and mixed states, we need a way of representing the weighted sum of a set of pure states (equivalently, of the probability functions associated with them) that is different from adding the (suitably weighted) vectors that represent them, and that means that we need either an alternative way of representing mixed states, or a uniform way of representing both pure and mixed states that preserves the distinction between them. There is a kind of operator in Hilbert spaces, called a density operator, that serves well in the latter capacity, and it turns out not to be hard to restate everything that has been said about state vectors in terms of density operators. So, even though it is common to speak as though pure states are represented by vectors, the official rule is that states – pure and mixed, alike – are represented in quantum mechanics by density operators.
Although mixed states can, as I said, be used to represent our ignorance of the states of systems that are actually in one or another pure state, and although this has seemed to many to be an adequate way of interpreting mixtures in classical contexts, there are serious obstacles to applying it generally to quantum mechanical mixtures. These are left for detailed discussion in the other entries on quantum mechanics in the Encyclopedia.
Everything that has been said about observables, strictly speaking, applies only to the case in which the values of the observable form a discrete set; the mathematical niceties that are needed to generalize it to the case of continuous observables are complicated, and raise problems of a more technical nature. These, too, are best left for detailed discussion.
This should be all the initial preparation one needs to approach the philosophical discussion of quantum mechanics, but it is only a first step. The more one learns about the relationships among and between vectors and operators in Hilbert space, about how the spaces of simple systems relate to those of complex ones, and about the equation which describes how state-vectors move through the space, the better will be one’s appreciation of both the nature and the difficulty of the problems associated with the theory. The funny backwards thing about quantum mechanics, the thing that makes it endlessly absorbing to a philosopher, is that the more one learns, the harder the problems get.
Bibliography
Books Useful For Beginners
Here are some recent books that will be especially useful to beginners.
- Norsen, T., 2017, Foundations of Quantum Mechanics: An
Exploration of the Physical Meaning of Quantum Theory, Cham:
Springer.
This is a textbook for students who want to learn quantum mechanics, but learn it in a way that emphasizes physical clarity. The book covers topics of a standard introduction to quantum physics, but focuses attention on questions of ontology often glossed over in standard texts. The physics student who wants to learn quantum mechanics either as preparation for studying foundations or simply in a way that looks for clear answers to questions like ‘What are the basic objects in the quantum world?’, ‘What kinds of configurations can they assume?’, ‘How do they move and interact with one another?’ can do no better than starting here.
- Susskind, L. and Friedman, A., 2014, Quantum Mechanics: The
Theoretical Minimum (2nd edition), New York: Basic Books.
At 384 pages, this book isn’t as pithy as the title would suggest. It provides very clear presentation of the principles of quantum mechanics for the physics student without any previous background. This is how one would learn quantum mechanics in a standard university course.
Helpful papers Deriving Quantum Mechanics from Simple Axioms
- Hardy, L., 2001 (v4), “Quantum Theory from Five Reasonable Axioms”, manuscript at arXiv.org.
- Schack, R., 2002 (v1), “Quantum Theory from four of Hardy’s Axions”, manuscript at arXiv.org.
- Darrigol, O., 2015, “‘Shut up and contemplate!’: Lucien Hardy’s reasonable axioms for quantum theory”, Studies in History and Philosophy of Science (Part B: Studies in History and Philosophy of Modern Physics), 52(B): 328–342.
Quantum Mechanics Textbooks
There are a great many textbooks available for studying quantum mechanics. Here are a few especially important ones with some notes to guide choices among them. It is good to work with two or three texts when learning QM. No text is perfect and differences in approach can illuminate the subject from different angles.
- Ballentine, L., 1998, Quantum Mechanics: A Modern
Approach, Singapore: World Scientific Publishing Company.
This book is not recommended for beginners, and not recommended as a textbook. It is recommended once one has some technical background to deepen understanding of the fundamental concepts of quantum mechanics.
- Basdevant, J.L., and J. Dalibard, 2005, Quantum
Mechanics, Berlin: Springer.
This is a brief, but elegant introduction. There aren’t a great many problems, but detailed solutions are provided for those that are included. The book comes with a CD-ROM that is very helpful for visualization.
- Dirac, P.A.M., 1930 [1958], The Principles of Quantum
Mechanics, Oxford: Clarendon Press, 1930; 4th edition, revised,
1958.
This is a classic, beautiful book that remains one of the clearest presentations of quantum mechanics. Everything is presented with extreme simplicity using Dirac’s formulation with non-commutative algebra. Even a beginner will be able to follow the presentation. The book emphasizes logical structure, in Dirac’s words: “problems were tackled top-down, by working on the great principles, with the details left to look after themselves.”
- Cohen-Tannoudji, C., 2006, Quantum Mechanics, New York:
Wiley-Interscience.
This is a comprehensive, encyclopedic text. It’s not the best to learn from, but is a good reference book.
- Gasiorowicz, S., 1995, Quantum Physics (3rd edition), New
York: Wiley.
This is a decent text, relatively well-written.
- Griffiths, D., 1995 [2018], Introduction to Quantum
Mechanics (2nd edition), Upper Saddle River, NJ: Prentice Hall;
3rd edition, 2018.
This is a standard undergraduate text for a first course in QM, and I would recommend it as a starting point for beginners. It is concise and very easy to read. There is an emphasis on conceptual development. Unfortunately, there are no worked examples in the book, and the answers to the problems are available only to instructors. It is easy to find and has recently been updated.
- Liboff, R., 1998, Introductory Quantum Mechanics (4th
edition), San Francisco: Addison-Wesley.
This is a nicely designed book, relatively well-written. It is a good starting point for beginners, but not at comprehensive as Shankar.
- Merzbacher, E., 1997, Quantum Mechanics (3rd edition),
New York: Wiley.
This is a standard graduate text in the US, not recommended for beginners, but quite good at an advanced level.
- Sakurai, J.J., 1993 [2021], Modern Quantum Mechanics
(revised edition), Reading, MA: Addison Wesley; third edition, with
coauthor Jim Napolitano, Cambridge: Cambridge University Press, 2021.
This is generally used as a graduate text. It is well-written and there is emphasis on experimental phenomena and important questions like Bell’s Inequality. The material is introduced at a higher level than Griffiths and Shankar, with lots of mathematics. There is a wealth of problems, but unfortunately few solutions are provided, making it most useful in a classroom setting or in conjunction with a book that contains worked examples and derivations.
- Schwinger, J., 2003, Quantum Mechanics (corrected
edition), Berlin: Springer.
This book is extremely mathematical in emphasis. There is less emphasis on conceptual development, and it is best used after one has acquired a conceptual understanding of QM and wants to see the mathematical development. The approach is very revealing. It is a difficult text, in part because some of the formalism is abstract and unconventional, but it is well worth the effort to comprehend. The problems throughout are excellent, but again unfortunately, solutions are not included in the text.
- Shankar, R., 1994, Principles of Quantum Mechanics (2nd
edition), Berlin: Springer.
This book is highly recommended as a starting point. It starts from ground zero, developing the mathematical tools needed to understand quantum mechanics. It is well written, and friendlier than Griffiths for students who are learning the subject on their own. QM is not introduced until page 115. The introductory chapter on linear algebra is very good. At 676 pages, it is comprehensive. It covers Feynman path integrals more thoroughly than other books, and contains solved problems. If you buy one book on QM, this is a good choice.
- Zettili, N., 2009, Quantum Mechanics: Concepts and
Applications, Chichester: John Wiley & Sons, Ltd.
This is a very good book as well. It covers theory and problem solving in an integrated way. It is easy to follow and full of problems and solutions that are related to the experimental basis of the theory.
Useful General Texts in Mathematics and Physics
Whether studying quantum mechanics on one’s own, or in a classroom setting, it is useful to have these books on hand as accompaniments. Even a seasoned teacher will find himself from time to time reaching for them:
- Benenson, W., J. Harris, H. Stoecker, , and H. Lutz, 2006, Handbook of Physics (2nd edition), Berlin: Springer.
- Bronshtein, I.N., and K.A. Semendyayev, 2007, Handbook of Mathematics (5th edition), Berlin: Springer.
- Halliday, D., R. Resnick, and J. Walker, 2008, Fundamentals of Physics (8th edition), Hoboken, NJ: Wiley.
- Halmos, P., 1957, Introduction to Hilbert Space (2nd edition), Providence: AMS Chelsea Publishing.
Books on Philosophy of QM
The last three decades have been a golden age for studying foundations of quantum Mechanics. Most of the active research is published in journals. The discussion surrounding standard non-relativistic quantum mechanics has stabilized in a way that makes it possible to survey. Three recent books absorb and organize the work of these decades.
- Barrett, J., 2019, The Conceptual Foundations of Quantum
Mechanics, New York: Oxford University Press.
This is a recent text on the history and conceptual foundations of quantum mechanics. It will serve an excellent primary text on the foundations of quantum mechanics for philosophy students, and will also make an excellent supplement to the standard quantum physics texts of physics students.
- Lewis, P., 2016, Quantum Ontology: A Guide to the Metaphysics
of Quantum Mechanics , New York: Oxford University Press.
Lewis’s book gives a very good presentation of the most influential and well-developed interpretations of the formalism and provides an even-handed comparative assessment. It provides is an up-to-date survey of the landscape with sophisticated analysis and commentary. The book is well-suited for use in or for the layperson with a serious interest in foundations. The discussion is sophisticated without undue technicality and manages philosophical analysis in a jargon-free way.
- Maudlin, T., 2019, Philosophy of Physics: Quantum Theory,
Princeton: Princeton University Press.
This is an excellent, if challenging introduction to quantum foundations. The book is unparalleled in clarity and uncompromising in its insistence on ontological intelligibility. It is more selective than Lewis and Barrett’s book (it covers Everettian Quantum Mechanics and Bohmian Mechanics and Spontaneous Collapse theories, but the Copenhagen approach is dismissed because it doesn’t have an explicit ontology). The author makes no bones about where his own sympathies lie, but it will reward the study of any beginning student or seasoned practitioner.
General Texts on the Philosophy of QM
- Albert, D., 1994, Quantum Mechanics and Experience, Cambridge, MA: Harvard University Press.
- Bell, J.S., 1987, Speakable and Unspeakable in Quantum Mechanics, Cambridge: Cambridge University Press.
- Busch, P., P. Lahti, and P. Mittelstaedt, 1991, The Quantum Theory of Measurement, Berlin: Springer-Verlag.
- Clifton, R.K. (ed.), 1996, Perspectives on Quantum Reality, Dordrecht: Kluwer.
- d’Espagnat, B., 1995, Veiled Reality, Reading, MA: Addison-Wesley.
- Hughes, R.I.G., 1989, Structure and Interpretation of Quantum Mechanics, Cambridge, MA: Harvard University Press.
- Omnès, R., 1994, The Interpretation of Quantum Mechanics, Princeton: Princeton University Press.
- Primas, H., 1983, Quantum Mechanics, Chemistry and Reductionism (2nd edition), Berlin: Springer.
- Rae, A., 1986, Quantum Physics: Illusion or Reality?, Cambridge: Cambridge University Press.
- Redhead, M.L.G., 1989, Incompleteness, Nonlocality and Realism, Oxford: Clarendon Press.
- Squires, E., 1990, Conscious Mind in the Physical World, Bristol, New York: Adam Hilger.
- Whitaker, A., 1996, Einstein, Bohr and the Quantum Dilemma, Cambridge: Cambridge University Press.
More Specialized Readings
- Becker, A., 2018, What is Real? The Unfinished Quest for the
Meaning of Quantum Mechanics, New York: Basic Books.
This is a retelling of the early history of quantum theory that describes how Bohr’s influence persuaded a generation of physicists that the demand for a clear account of quantum ontology was somehow inappropriate. The book is a gripping tale of a turbulent time in the history of physics, when personalities clashed as deeply as philosophical sympathies.
- Carroll, S., 2019, Something Deeply Hidden: Quantum Worlds and
the Emergence of Spacetime, New York: Dutton.
This is a lively development and well-written defense of the Everettian viewpoint that looks beyond standard non-relativistic theory and argues that the real lesson of quantum conundra and their reconciliation of quantum mechanics with General Relativity is the recognition that space-time is not fundamental.
Academic Tools
How to cite this entry. Preview the PDF version of this entry at the Friends of the SEP Society. Look up topics and thinkers related to this entry at the Internet Philosophy Ontology Project (InPhO). Enhanced bibliography for this entry at PhilPapers, with links to its database.
Other Internet Resources
- Preskill, J., 1998, Quantum Computation (Lecture Notes for Physics 219, California Institute of Technology)


